Convoltional Neural Network 강의 내용 part.A

본 포스트는 Hands-on Machine learning 2nd Edition, CS231n, Tensorflow 공식 document를 참조하여 작성되었음을 알립니다.

Index

1. Introduction of Convolution Operation
2. Definition of Convolutional Neural Network(CNN)
3. Back Propagation of CNN
4. Partice

여기서는 1~3는 Part. A이고 4은 Part. B에서 다루도록 하겠다.

Introduction of Convolution Operation

---

Convolutional Neural Network는 Convolution 연산을 Neural Network에 적용한 것이다. 따라서 이를 알기 위해서는 Convolution 연산을 먼저 알아야할 필요가 있다. 관련 학과 대학생이라면 아마도 신호와 시스템을 배우면서 이를 처음 접했을 것이다. Continuous domain, Discrete domian까지 이 연산을 정의될 수 있고 각각에 따라 계산 방법 또한 배웠을 것이다. 예를 들어서 2차원의 Image와 2차원의 Filter의 Convolution 연산을 수식으로 표현해 보도록 하겠다.

• Image 행렬 정의

$$I(i, j)$$

Image의 $i$열, $j$행의 성분

• Filter 행렬 정의

$$K(i, j)$$

Filter의 $i$열, $j$행의 성분. 높이를 $k_1$, 너비를 $k_2$라고 가정.

• $I$와 $K$의 Convolution 연산

$$(I*K)_{ij} = \sum_{m = 0}^{k_1 - 1} \sum_{n = 0}^{k_2 - 1}I(i - m, j - n)K(m, n) \tag{equation (1)}$$

위 정의를 조금 틀면 다음과 같이도 표현이 가능하다.

$$(I*K)_{ij} = \sum_{m = 0}^{k_1 - 1} \sum_{n = 0}^{k_2 - 1}I(i + m, j + n)K(-m, -n) \tag{equation (2)}$$

위와 같은 연산의 형태를 Correlation이라고 한다. 즉, Convolution 연산의 Filter를 $\pi$만큼 회전시킨다면 그것이 Correlation 연산인 것이다. 이는 아주 중요한 관계이므로 꼭 기억해 두도록 하자.

Definition of Convolutional Neural Network(CNN)

---

CNN의 정의는 위의 Convolution 연산을 사용하여 Weight와 Input을 계산하는 것이다. 매우 간단한 예시로 LeNet이라는 것을 보자. 너무 자주 나오는 예시라서 하품이 나올 것 같지만, 본래 기본이라는 것은 “쉬운”것이 아니라 “중요한”것이다.

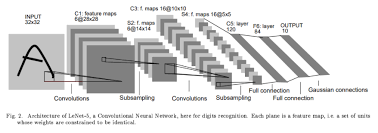
그림에서의 각 파트를 분해해서 살펴보면 다음과 같다.

Image Input -> (Convolution) -> Feature Map -> (Pooling) -> Feature Map -> (Convolution) -> Feature Map -> (Pooling) -> Feature Map -> (Flatten) -> Feature Vector -> (FCNN) -> Feature Vector -> (FCNN) -> Feature Vector -> (Gaussian Connection) -> Output Vector

여기서 괄호 안에 들어 있는 것이 연산의 이름이다. FCNN은 다른 포스트에서 봤다고 가정하고, 여기서 주목해야 할 것은 Pooling Layer이다.

Pooling은 다양한 종류가 있는데 간단하게 한가지만 소개하자면 Max Pooling이 있다. 자세한 것은 Tensorflow 2 공식 문서를 참조하는 것이 더 좋을 것 같다.
여기서는 Pooling까지 자세히 다룰 이유는 없는 것 같다.

이제 본격적으로 Convolution 연산에 대해서 알아보도록 하겠다. 그 전에 FCNN 포스트에서도 그랬듯이, 수식 표현을 하기 위한 정의부터 하고 시작하자.

Definition 1

• $u_{ijm}^l$: $l$번째 층의 Feature Map의 $m$번째 Channel $i$행, $j$열의 성분
• $x_{ijm}$: Input의 $m$번째 Channel의 $i$행, $j$열의 성분
• $w_{ijmk}^l$: $l$번째 층의 Weight의 $k$번째 Kernel Set에 $m$번째 Channel, $i$행, $j$열의 성분
• $b_m^l$: $l$번째 층의 $m$번째 Channel의 Bias

이를 통해서 Convolution Layer를 수학적으로 표현해 보자면 다음과 같다.

$$u_{ijm}^l = \sum^{H - 1}_{p = 0} \sum^{W - 1}_{q = 0} \sum^{K - 1}_{k = 0} z^{l - 1}_{i+sp,j+sq,k}w^l_{p,q,k,m} + b^l_m \tag{equation (3)}$$

여기서 $z$행렬은 $u$행렬에 activation function을 씌워 놓은 것이라고 생각하면 편하다.

이를 그림으로 표현해보면 다음과 같다.

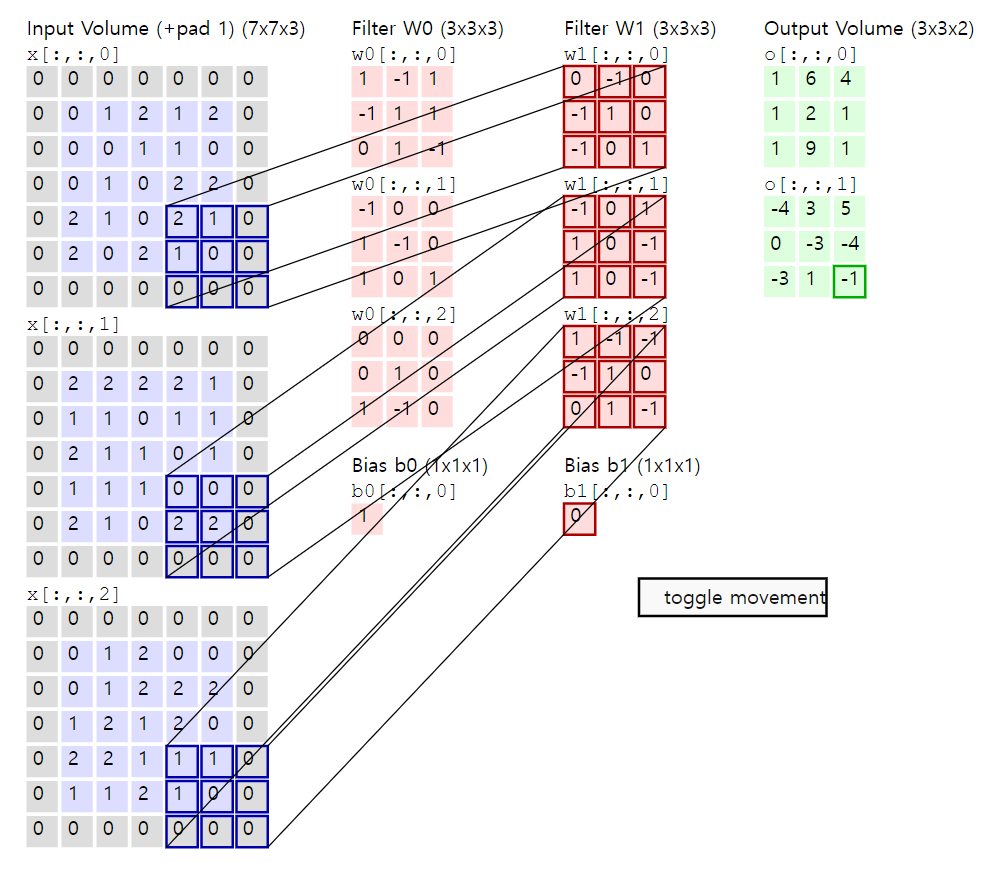
위 수식에서는 아직 정의되지 않은 부분, 설명되지 않은 부분이 많다. 첫번째로 $H$, $W$, $K$의 의미, 그리고 index 부분의 $s$의 의미이다. 또한, 위의 연산은 Correlation인데 왜 Convolution 연산이라고 하는 것일까?

일단 첫번째는 $H$, $W$, $K$인데, 이는 각각 Weight의 높이, 너비, 채널수이다. 그리고 index 부분의 $s$는 Stride이다. Convolution 연산의 Weight를 옮겨가면서 곱셉을 할때 얼마나 옮길지를 결정한다. 이 값을 키울수록 결과 이미지의 크기가 작아진다. 자세한 것을 하나하나 까볼려면 오래 걸리니, 이 부분은 혼자서 잘 생각해 보는게 좋을 것 같다. 어디까지나 이 문서는 입문서가 아니라는 점을 알아주었으면 좋겠다. 기존에 Tensorflow/Pytorch만을 사용하던 사람들에게 이론을 제공하고자 함이다.

Back Propagation of CNN

---

자. 본격적으로 어려운 부분이다. 앞으로 Deep learning 강의를 써내려가면서 이보다 어려운 부분은 없다. 그리고 필자가 생각하기에도 쓸모가 없다. 단지 지적 유희를 위해서 읽어주기를 바라며 틀린 부분이 있다면 지적해 주기를 바란다.

그 전에, 왜 필자는 굳이 이 파트를 써내려 가는가를 적어보도록 하겠다. (잡담이니 굳이 안 읽어도 상관 없다.) 최근의 Deep learning 개발은 Auto Grad 계열의 알고리즘들을 활용하여 앞먹임 연산만을 정의하면 알아서 역전파 수식이 계산되어 BackPropagation을 편리하게 할 수 있다. 하지만 라이브러리에 모든 것을 맡기고 개발만 하는 것이 과연 좋은 개발자/연구원 이라고 할 수 있을까? 필요하다면 더 깊은 인사이트를 얻어서 문제를 해결해야할 필요가 있다. 이 글은 그런 사람들을 위함이기도 하고 나처럼 학문 변태들을 위한 것이기도 하다. 그러니 이 파트가 필요 없다고 판단되면 읽지 않는 것을 추천하고, 만약 틀린 것이 있다면 부디 연락해서 알려주었으면 좋겠다. 환영하는 마음으로 받아들이고 수정하도록 하겠다.

사족이 길었는데, 그래서 Back Propagation이 어떻게 정의되는 것일까? 큰 틀은 FCNN과 다를 바가 없다. Weight를 업데이트함에 있어서 Chain Rule을 활용하는 것이다. 그렇다면 어떻게 그것을 진행할 것인가?
우선 첫번째로 미분부터 써내려 가보자.

$$\frac{\partial E}{\partial w^l_{ijmk}} \tag{def 2}$$

이것을 구해서 Weight를 업데이트하는 것이 Back Propagation의 핵심이다. 그렇다면 FCNN과 똑같이 일반화된 Delta Rule을 활용해 보는 것으로 시작하자. 이를 위해서 chain rule을 적용해 보면 다음과 같이 표현할 수 있다.

$$\frac{\partial E}{\partial w^l_{ijmk}} = \sum_{p=0}^{H'}\sum_{q=0}^{W'} \frac{\partial E}{\partial u^l_{pqm}}\frac{\partial u^l_{pqm}}{\partial w^l_{ijmk}} \tag{equation (4)}$$

이때, $H’$, $W’$는 Convolution output의 결과 Feature map의 높이와 너비이다.
FCNN때와 똑같이 한다면 다음과 같이 Delta를 정의하고 식을 수정할 수 있다.

$$\delta_{pqm}^l = \frac{\partial E}{\partial u^l_{pqm}} \tag{def 3}$$

그리고 다음과 같이 식을 유도하는 것이 가능하다.

$$\frac{\partial E}{\partial w^l_{ijmk}} = \sum_{p=0}^{H'}\sum_{q=0}^{W'} \delta_{pqm}^l \frac{\partial u^l_{pqm}}{\partial w^l_{ijmk}} = \sum_{p=0}^{H'}\sum_{q=0}^{W'} \delta_{pqm}^l z^{l - 1}_{i+sp, j+sq, k} \tag{equation (5)}$$

결국 다음과 같이 표현 가능하다.

$$\frac{\partial E}{\partial w^l_{ijmk}} = (\delta_{m}^l * z^{l-1}_k)_{ij} \tag{equation (6)}$$

이제 delta를 정의했으니, 앞층의 delta와 뒷층의 delta간의 관계를 밝혀내서 연산을 효율화 하면 된다. 이 과정을 손으로 유도하는 것은 필자가 생각해도 실용적 측면에서는 정말 쓸데가 없다. 왜냐하면 현대의 신경망 구조는 너무 복잡해져서 이걸 유도했다 쳐도 다른 구조들이 정말 많이 때문에 써먹을 수가 없기 때문이다. 하지만 아주 제한적인 경우에 대해서 이걸 유도해 보도록 하겠다.

1. Convolution - Convolution layer 에서의 Delta 점화식

우선 다시 한번 delta에서 chain rule을 적용해 보도록 하겠다 . 이 과정은 FCNN에서도 했을 것이다. 따라서 최대한 간결하게 진행해 보도록 하겠다.

$$\frac{\partial E}{\partial u^l_{pqm}} = \sum_{x=0}^{H''}\sum_{y=0}^{W''} \sum_{c=0}^{C''} \frac{\partial E}{\partial u^{l + 1}_{p - sx,q - sy, c}} \frac{\partial u^{l + 1}_{p - sx,q - sy, c}}{\partial u^l_{pqm}} \tag{equation (7)}$$

이때 $H’’$, $W’’$, $C’’$는 다음 층에서의 Feature Map의 크기이다.

이를 전개해 보면 다음과 같다.

$$\frac{\partial E}{\partial u^l_{pqm}} = \sum_{x=0}^{H''}\sum_{y=0}^{W''} \sum_{c=0}^{C''} \delta_{p-sx,q-sy,c}^{l+1} w^{l+1}_{xycm} f'(u^{l}_{pqm}) \tag{equation (8)}$$

이는 다음과 같이 Convolution 연산으로 표현될 수 있다.

$$\frac{\partial E}{\partial u^l_{pqm}} = (\delta^{l+1} * w_m^{l+1}) \odot f'(u^l_m) \tag{equation (9)}$$

위의 $\odot$은 성분 끼리의 곱(element wise multiplication)을 의미한다.

1. Convolution - Pooling - Convolution 에서의 Delta 점화식

위에서 delta를 유도함에 있어서 한 층이 더 추가될 뿐이다. 다음과 같이 말이다. 여기서는 Max Pooling, Average Pooling을 예로 들어보겠다.

$$\frac{\partial E}{\partial u^l_{pqm}} = \sum_{x=0}^{H''}\sum_{y=0}^{W''} \sum_{c=0}^{C''} \frac{\partial E}{\partial u^{l + 2}_{p' - sx,q' - sy, c}} \frac{\partial u^{l + 2}_{p' - sx,q' - sy, c}}{\partial u^{l + 1}_{p'q'm}} \frac{u^{l + 1}_{p'q'm}}{u^l_{pqm}} \tag{equation (10)}$$ $$\frac{\partial E}{\partial u^l_{pqm}} = \sum_{x=0}^{H''}\sum_{y=0}^{W''} \sum_{c=0}^{C''} \delta_{p-sx,q-sy,c}^{l+1} w^{l+1}_{xycm} \frac{\partial u^{l + 2}_{p' - sx,q' - sy, c}}{\partial u^{l + 1}_{p'q'm}} f'(u^{l}_{pqm}) \tag{equation (11)}$$

위 식에서 중간에 있는 $l+1$층이 Pooling 층이다. 이 미분은 다음과 같이 정의된다.

• Max Pooling의 경우

$$\frac{\partial u^{l + 2}_{p' - sx,q' - sy, c}}{\partial u^{l + 1}_{p'q'm}} = \begin{cases} 1 \space \space \space \space \space \text{if p, q 성분이 최댓값이었을 경우} \\ 0 \space \space \space \space \space \text{otherwise} \end{cases} \tag{equation (12)}$$

• Average Pooling의 경우

$$\frac{\partial u^{l + 2}_{p' - sx,q' - sy, c}}{\partial u^{l + 1}_{p'q'm}} = \frac{1}{H''' * W'''} \tag{equation (12)}$$

여기서 $H’’’$,$W’’’$는 Pooling Layer의 크기이다.

결국 Pooling layer까지 포함하면 다음과 같이 convolution 연산으로 정의할 수 있다.

$$\delta_{pqm}^l = \text{Upsampling}[(\delta^{l + 2} * w^{l + 2}_m)] \odot f'(u^l_m) \tag{equation (13)}$$

어디까지나 이렇게 연산을 할 수 있는 이유는 Pooling layer는 업데이트를 할 필요가 없기 때문이다. 만약 업데이트를 할 피라미터가 있다면 “제대로” 다시 delta rule의 방정식을 수정해 줘야 한다.

1. 이게 정말 쓸데 없는 이유

현대의 신경망은 에시당초 Convolution layer에서 탈각하는 분위기 인데다가 Convolution - Feed Forward 관계나 ResNet같은 현대의 신경망 구조에서는 이런 복잡한 수식으로 구현하는 것은 사실상 불가능에 가깝다. 그러니 우리는 Autograd를 믿고 이런건 그냥 지적 유희로만 알아 두도록 하자.

그리고 마지막으로 Bias의 Update 방법을 알아보면 다음과 같다.

$$\frac{\partial E}{\partial b_m^l} = \sum^{H_o - 1}_{p = 0} \sum^{W_o - 1}_{q = 0} \frac{\partial E}{\partial u_{pqm}^l} \frac{\partial u_{pqm}^l}{\partial b_m^l} \tag{equation (14)}$$

이때, 곱셈 term의 뒷 항은 전부 1이므로 다음과 같은 식이 성립한다.

$$\frac{\partial E}{\partial b_m^l} = \sum^{H' - 1}_{p = 0} \sum^{W' - 1}_{q = 0} \delta_{pqm}^l \tag{equation (15)}$$

이걸로 CNN의 이론 부분은 끝났다. 다음에는 실습 부분으로 찾아오도록 하겠다.