Fully Connected Neural Network 강의 내용 part.A

본 포스트는 Hands-on Machine learning 2nd Edition, CS231n, Tensorflow 공식 document를 참조하여 작성되었음을 알립니다.

Index

1. Basic of Neural Network
2. Definition of Fully Connected Neural Network(FCNN)
3. Feed Forward of FCNN
4. Gradient Descent
5. Back Propagation of FCNN
6. Hyper parameter tuning
7. Partice

여기서는 1~5는 Part. A이고 6,7은 Part. B에서 다루도록 하겠다.

Basic of Neural Network

---

Neural Network의 기본을 설명할때 항상 나오는 것이 바로 뉴런 구조 사진이다. 여기서는 그들을 생략하도록 하겠다. 굳이 여기서 설명할 필요를 못 느끼겠다.
궁금하면 SLP(Single Layer Perceptron)와 MLP(Multi Layer Perceptron)에 대해서 구글링을 해보도록 하자.

우선 FCNN을 본격적으로 들어가기 전에, 지도 학습에 대한 Deep learning의 학습 프로세스에 대한 개략적인 모식도를 보고 가자.

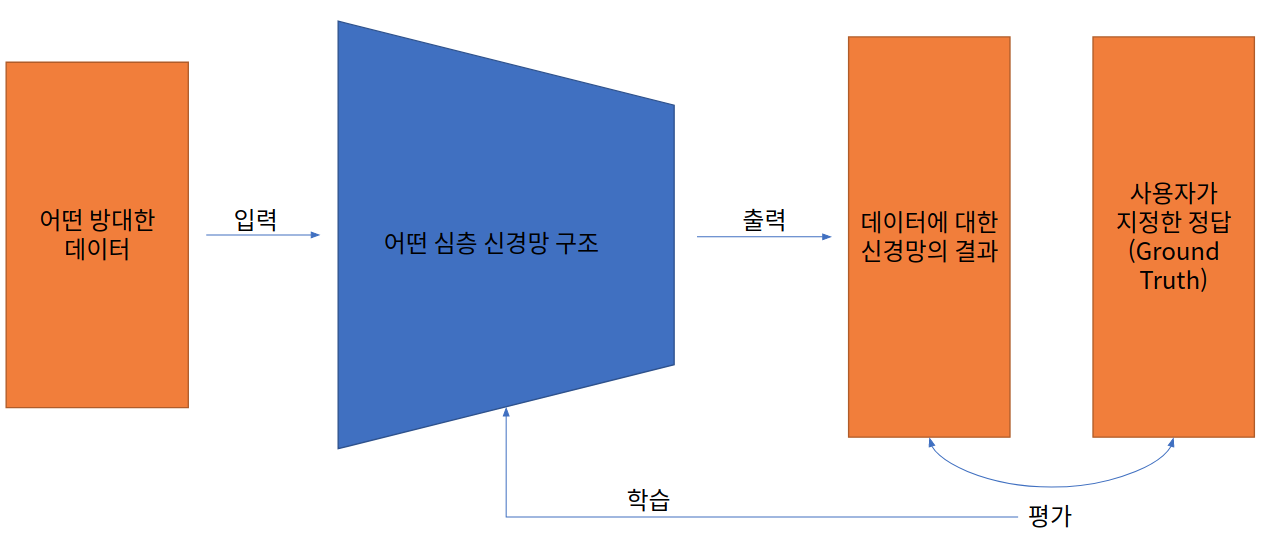
이러한 모식도에 개략적인 생략이 들어 갔고, 반례도 충분히 있겠지만, 지도 학습의 형태로 학습하는 대부분의 Neural Network는 이런 Process로 학습을 하게 된다.
앞으로 나오는 신경망 구조들 중에서 위의 “출력”, “평가”, “학습”의 3가지의 과정을 집중적으로 기술할 생각이다.

그렇다면 Neural Network 구조를 활용해서 풀 수 있는 문제는 무엇이 있을까?
여기서는 크게 2가지만 다룰 예정이다.

1. Classification: 어떤 입력을 특정 범주로 분류해내는 문제.
2. Regression: 어떤 변수들 사이의 관계를 도출해내는 문제. (Modeling에 가깝다고 생각하면 편함.)

이러한 2개의 문제의 범주를 설명하고 넘어가는 이유는 Neural Network로 어떤 문제를 풀 것이냐에 따라서 학습 과정에서 다양한 부분이 상이하게 변하기 때문이다. 이는 나중에 따로 자세하게 다룰 예정이다. 지금은 일단 이런 것이 있다 라는 것만 알아두고 가자.

Definition of FCNN

---

여기서는 Fully Connected Nueral Network의 정의를 먼저 알아보도록 하겠다. 간단하게 이를 표현하자면 다음과 같은 구조를 가지는 Neural Network를 일컫는다.

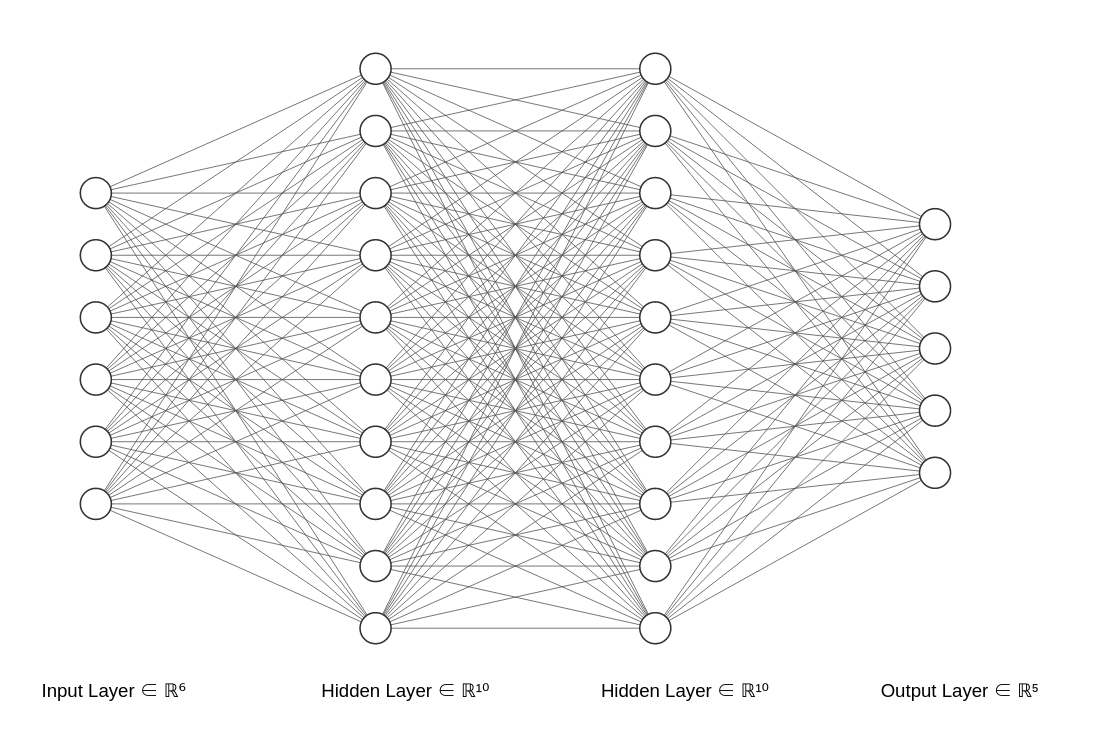
Figure 1: FCNN의 모식도 1
이렇게 앞층의 뉴런과 뒷층의 뉴런이 빠짐없이 전부 연결된 구조를 FCNN이라고 한다. 여기서 만약 독자가 MLP를 모르는 상태라면 위의 구조가 상당히 추상적으로 다가올 것이다. 간단하게 생각해서, 각 뉴런들은 숫자를 가지고 있다고 생각하면 된다. 다음 그림을 보면 훨씬 쉽게 이해할 수 있다.

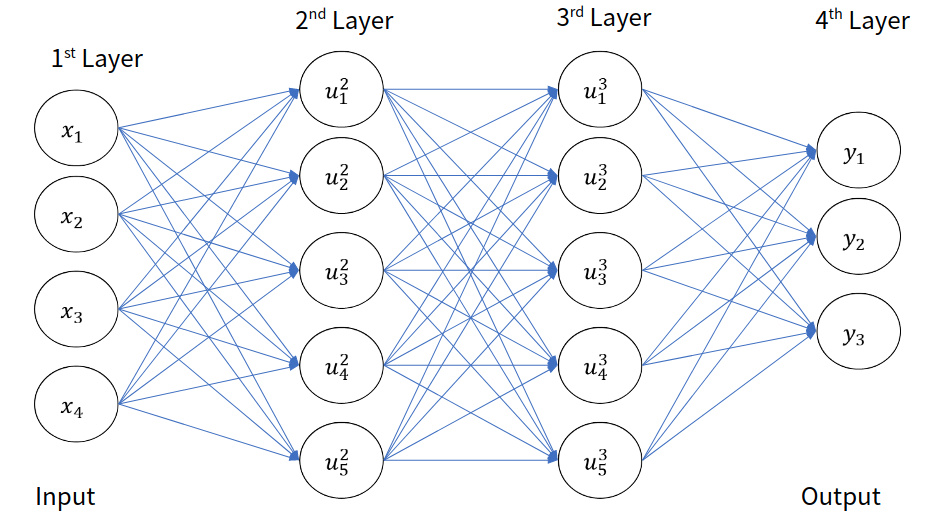
Figure 2: FCNN의 모식도 2

이렇게 층의 뉴런마다 간선으로 연결되어 있고 각 뉴런들은 뒤의 뉴런들에게 어떠한 가중치를 반영해서 자신의 값을 가지고 있다고 생각하면 된다. 이제부터 우리는 이러한 구조를 가진 Neural Network가 어떻게 주어진 문제에 대해서 결과를 도출하고 학습을 진행하는지 알아보도록 하겠다.

Feed Forward of FCNN

---

이 과정은 학습이 되었건 되지 않았건 FCNN의 구조에서 입력을 통해 출력을 얻어내는 과정이다. 층층이 쌓인 Neural Network 구조에서 앞으로 계속 나아가면서 결과를 도출해 내는 모습에서 Feed Forward(앞 먹임)이라는 이름이 붙은 것이다.
앞으로 대부분의 예시는 Figure 2와 비슷한 형식으로 나올 것이다. 그리고 앞으로는 뉴런이라는 명칭보다는 Unit이라는 명칭을 사용할 것이다.
이제, 이전 슬라이드에 있는 것들을 기호를 명확하게 정의해 보도록 하겠다.

Definition 1

• $x_i$: 입력 벡터의 $i$번째 원소
• $u_i^k$: $k$번째 Layer의 $i$번째 Hidden Units의 값.
• $w^k_{ij}$: $k$번째 층의 $i$번째 Unit과 $k-1$번째 층의 $j$번째 Unit을 이어주는 가중치
• $y_i$: 출력층의 $i$번째 Unit
• $n_k$: $k$번째 층의 Unit의 갯수

그렇다면 이제 Feed Forward를 위해서 가장 중요한 부분을 설명하도록 하겠다. Weighted Sum(가중합)에 대한 부분이다.
앞선 Figure 1과 Figure 2에서 앞층과 뒷층의 관계를 우리는 다음과 같이 정의한 것이다.

$$u_i^k = \sum_{j=1}^{n^{k-1}}w^k_{ij}u^{k-1}_j \tag{Equation (2)}$$

정말 단순하게 생각해서 이전 유닛에 해당하는 가중치만큼 앞의 유닛에 반영해 주면 되는 것이다. 이렇게 뒤의 층에서 앞의 층으로 순차적으로 계산해 나가면 된다.

하지만 여기에는 치명적인 문제점이 있다. 바로, 이렇게 된다면 Neural Network 구조로 Linear Function 밖에 표현할 수 없다는 것이다.
위의 $equation (1)$의 형식으로 Feed Foward를 진행하게 된다면 층을 쌓는 것이 의미가 없어진다. 그 이유는 단순히 일변수 선형 함수를 생각해보면 알 수 있다.
우리가 $y = a_ix$라는 임의의 $N$개의 함수들을 층층이 쌓는다 할저언정 그것은 새로운 선형 함수 $y = a’x, \quad a’ = a_1a_2a_3\cdot\cdot\cdot a_N$ 를 만들어 내는 것과 별반 다를 것이 없다. 이렇게 되면 가장 대표적인 문제점은 바로 XOR문제를 해결할 수 없다는 것이다. 이는 너무 보편적인 문제라서 그냥 구글링 하면 나보다 설명 잘해놓은 글이 널려있다. 따라서 여기서는 생략한다.
똑같은 논리이다. 이에 대한 자세한 논의는 Appendix. A에 자세히 기술하도록 하겠다.

이러한 문제를 해결하고 더 다양한 함수를 신경망이 표현할 수 있게 하기 위해서 Activation function과 Bias를 적용하게 된다.

Activation Function(활성 함수)

신경망이 Linear한 함수만을 근사시키는 것을 방지하기 위해서 중간에 Non Linear Function을 Unit에 적용하게 된다. 이때 이러한 함수를 Non linear function이라고 한다. 그렇다고, 전부 Non linear인 것은 아니다. 하지만 Non linear function이여야 앞선 문제가 발생하지 않을 것이다. 그 종류는 대략 다음과 같다.

1. Sigmoid: $\sigma(x) = \frac{1}{1+\exp(-x)}$
2. ReLU(Rectified Linear Unit): $max(0, x)$
3. Leaky ReLU: $max(0.1x, x)$
4. Hyperbolic tangent: $\tanh(x) = \frac{\exp(x) - \exp(-x)}{\exp(x) + \exp(-x)}$
5. ELU(Exponential Linear Unit): $\sigma(x) = xu(x) + a(\exp(x)-1)u(-x)$

이것 뿐만 아니라 진짜 개 많다. 나머지는 Tensorflow 공식 Document나 구글링을 통해서 알아보도록 하라.

이렇게 Activation Function을 씌운 값을 앞으로는 다음과 같이 표현하도록 하겠다.

Defintion 2: 활성함수를 적용한 Unit의 값.

$$z_i^k = f(u^k_i)$$

Bias (편향)

Bias로써는 Non Linear성을 신경망에 추가할 수는 없다. 하지만 Activation Function을 평행 이동 시켜주는 역할을 하게 해서 입력이 0인 지점에서의 신경망의 자율도를 높여주게 된다. 예를 들어보자. 위에 예시를 든 Activation function들에서는 예를 들어서 $(0, 32)$같은 점을 표현할 수 없다. 그렇기 때문에 Bias를 주어서 평행 이동을 시켜주는 것이다. 이것의 유무가 신경망의 학습 양상과 성능이 크게 차이를 주는 경우가 많다.

즉, 최대한 많은 함수를 근사할 수 있도록 위와 같은 설정을 추가해 주는 것이다.
이러면 어떤 잼민이는 이런 질문을 할 수 있을 것이다.

???: 아 ㅋㅋㅋㅋ 그런 근사 못 하는 함수는 어쩔건데요 ㅋㅋ루삥뽕

걱정 마라. 이미 만능 근사 정리(Universal Approximation Theorem, 시벤코 정리)에 의해서 증명되었다. 그냥 안심하고 쓰면 된다.

그렇다면 Bias를 적용해서 다시금 Unit의 값을 작성해 보자.

Definition 3: Bias를 적용한 Unit의 값

$$u_i^k = \sum_{j=1}^{n_{k-1}}w^k_{ij}z^{k-1}_j + b^k_i \tag{Equation (2)}$$

Figure 3: Bias를 반영한 Neural Network의 표현

이제 이를 행렬로 표현해보자. 행렬로써 표현하여 식을 짧고 간편하게 정리할 수 있으며, 컴퓨터에서의 구현을 다소 직관적이고 편하게 할 수 있다.

$$U^k = \begin{bmatrix} u^k_1 && u^k_2 && \dots && u^k_{n_k} \end{bmatrix} ^T \tag{Def. 4}$$

$$W^k = \begin{bmatrix} w^k_{11} && w^k_{12} && \cdots && w^k_{1n_{k-1}} \\ w^k_{21} && w^k_{22} && \cdots && w^k_{2n_{k-1}} \\ \vdots && \ddots && \ddots && \vdots \\ w^k_{n_k1} && w^k_{n_k2} && \cdots && w^k_{n_kn_{k-1}} \\ \end{bmatrix} \tag{Def. 5}$$

$$Z^{k-1} = \begin{bmatrix} z^{k-1}_1 && z^{k-1}_2 && \dots && z^{k-1}_{n_{k-1}} \end{bmatrix}^T \tag{Def. 6}$$

$$B^k = \begin{bmatrix} b^k_1 && b^k_2 && \dots && b^k_{n_k} \end{bmatrix}^T \tag{Def. 7}$$

$$\therefore U^k = W^kZ^{k-1} + B^k \quad (Z^k = f(U^k), \quad where \space f: \mathbb{R}^{n^k} \to \mathbb{R}^{n^k})$$

Gradient Descent

---

이번 장에서는 Gradient Descent에 대해서 다룰 예정이다. 하지만 너무 깊게는 안 다룰 생각이다. 그렇다고 걱정할 필요는 없다. 나중에 존나 자세하게 다룰거니깐 걱정은 붙들어 매도록 하자.

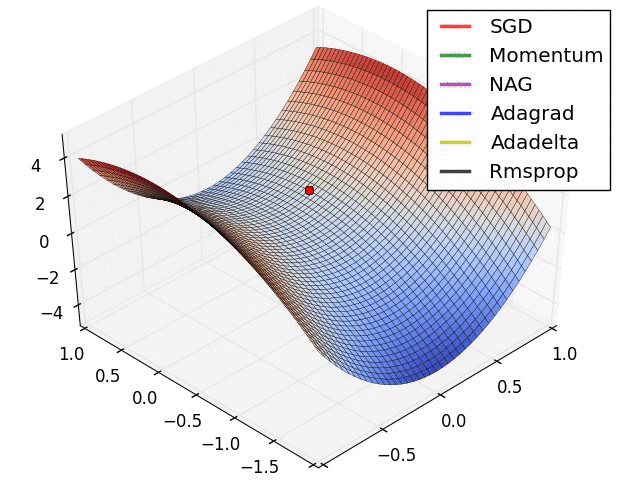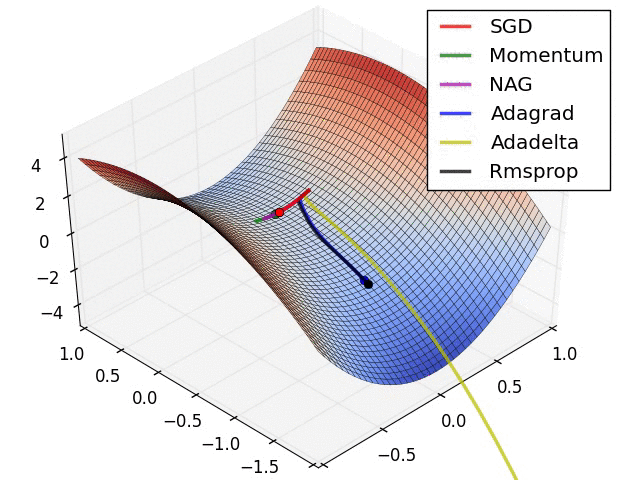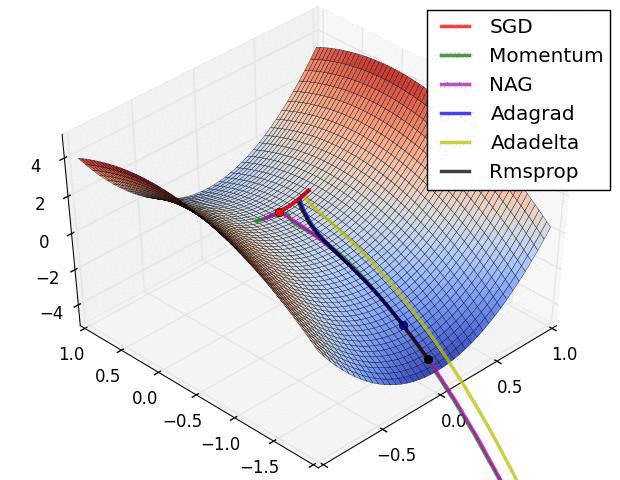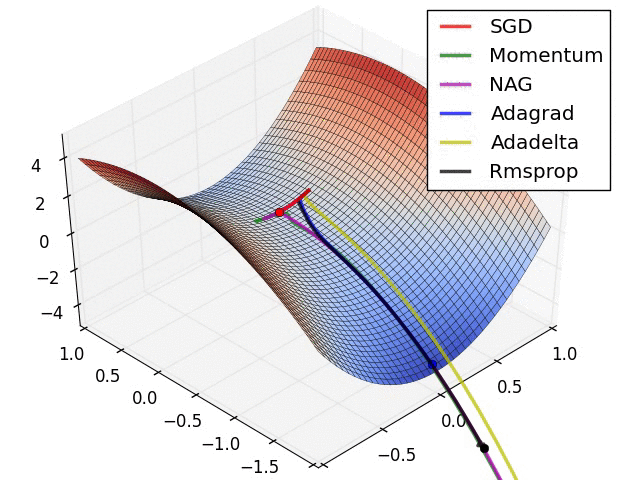
Figure 4. Gradient Descent을 묘사하는 Figure
Gradient Descent는 간단하게 설명해서 Gradient를 활용해서 Objective Function(목적 함수)의 최저점을 찾는 것이 목표이다. 위의 사진처럼 말이다. 이의 명확한 표현을 직관적으로 납득시키기 위해서 다음의 사진을 보자.

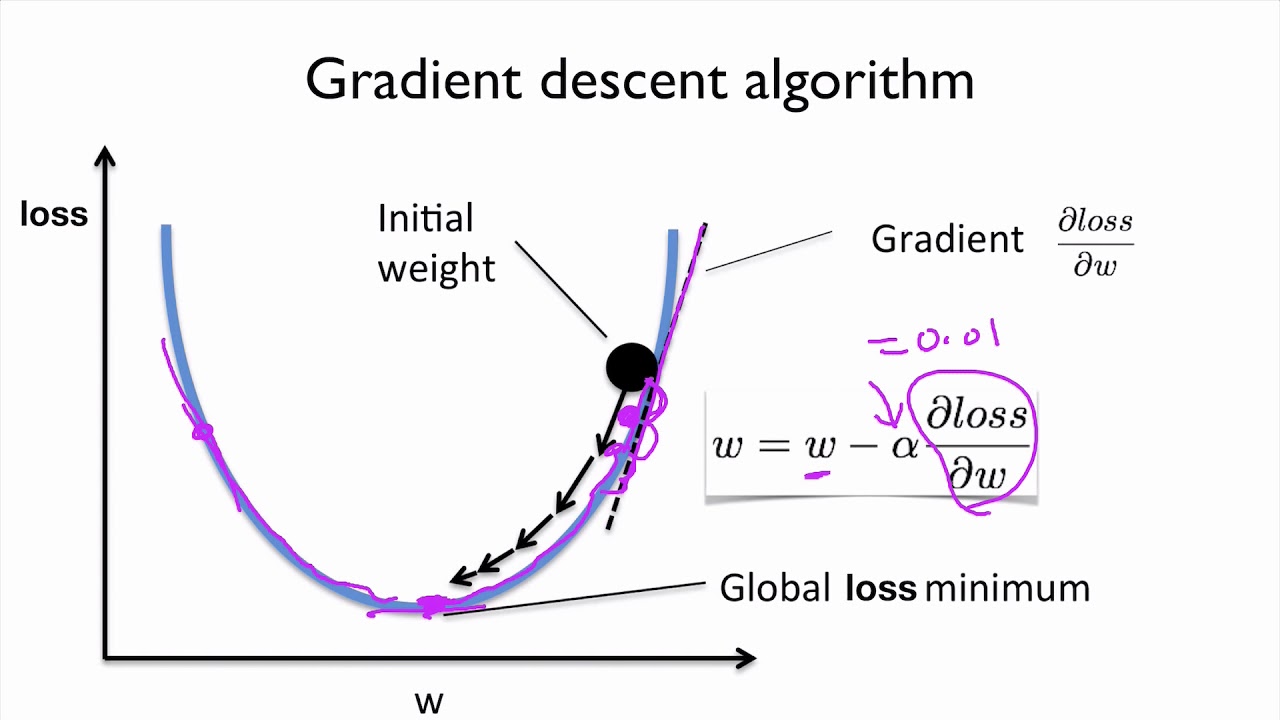
Figure 5. Gradient Descent를 직관적으로 설명하기 위한 그림

이처럼 목적 함수의 미분값을 활용하여 목적 함수의 최저점을 찾는 것이 가능하다. 이에 대한 자세한 설명은 진짜 나중에 질리도록 해주도록 하겠다. 걱정하지 말아달라.

그렇다면 이제 Neural Network에서 목적 함수는 어떤 것을 사용하는지 알아봐야한다. 이것도 지금은 그냥 “그런 것이 있다”라고만 생각하자. 이 파트는 신경망을 이해하는데 있어서 중요하고 심도있는 내용이기 때문에 나중에 Post 하나를 통으로 열어서 집중적으로 설명할 것이다.

이번 포스트에서는 목적함수로써 주로 2가지를 다룰 것이다.

1. Mean Squared Error

$$E = \frac{1}{2N}\sum_i(y_i - t_i)^2 \tag{Equation (3)}$$

1. Cross-Entropy

$$E = -\sum_c t_c\ln y_c \tag{Equation (4)}$$

$Equation 3$은 주로 regression 문제에서 목적 함수로 쓰이고, $Equation 4$는 주로 classification 문제에서 쓰인다.
이렇게 Error function이 있는데 Update를 어떻게 한다고 하는 것일까? 다음과 같은 공식으로 Update 하면 된다

$$w_{t+1} \gets w_t - \alpha \frac{\partial E}{\partial w_t} \quad \alpha: learning \space rate \tag{Equation (5)}$$

직관적으로 생각해보면, 그래프의 미분값이 음수이면 아래로 볼록한 이차 함수에서 극소점이 오른쪽에 있다는 것이다. 그렇다면 변수에 양수를 더해줘야 극소점에 다가갈 것이다. 반대도 마찬가지이다. 그리고 한번 Update를 할때 너무 변화폭을 급하게 하지 않기 위해서 learning rate를 곱해줘서 update를 해준다. 그렇게 적절한 learning rate를 지정하여 몇번 반복해주면 최저점에 수렴해 있을 것이다.

집요하지만, 이번 주제에 관한 내용은 나중에 “Optimization, Error function, and Problem”에 관한 포스트에서 자세하게 다룰 것이다. 그러니 지금은 직관적으로만 학습의 Process를 이해하는데 사력을 다해주기를 바란다.

Back-propagation of FCNN

---

이번에는 어떻게 신경망에 Gradient Descent를 적용할 것인지에 대한 내용이다. 위의 Gradient Descent를 배운 사람이라면 $Equation 5$를 활용하여 가중치의 Update를 다음과 같이 해줘야 할 것이라는데 이견을 가지지는 않을 것이다.

$$w^m_{ij} \gets w^m_{ij} - \alpha \frac{\partial E}{\partial w^m_{ij}} \tag{Equation (6)} \quad , m \in [1, K] \cap \N$$

여기서 $K$는 층의 갯수이다.

이때 수치해석을 공부한 사람이라면, 다음과 같은 말을 할 수 있다.

적당한 $\epsilon$을 선택하고, 수치 미분을 해주면 되지 않을까?

뭐, 틀린 말은 아니다. 실제로도 좋은 방법이 될 수 있다.(신경망이 아니라면 말이지) 하지만 이건 Neural Network이다. 미친 연산량을 자랑하는 이쪽 바닥에서 안이하게 접근했다가는 피를 볼 수 있다.
요즘은 많은 알고리즘들이 발달해서 어떨지는 모르지만, 기본적인 수치 미분은 여기서 좋은 방법이 아니다. 우선 수치 미분을 진행하는 방법은 다음과 같다.

$$\frac{df}{dx} \approx \frac{f(x+\epsilon) - f(x)}{\epsilon}$$

우선 이걸 신경망에 적용시키기 위해 가장 먼저 떠오르는 방법은 다음과 같을 것이다.

1. $f(x+\epsilon)$를 계산한다.
2. $f(x)$를 계산한다.
3. 미분을 계산한다.

자, 1,2번의 과정을 신경망에 적용해 주려면 당신은 2번의 함수 값을 계산해 줘야한다. 만약, 계산량이 크지 않은 함수라면 빨리 되겠지만, 이건 신경망이다. Figure 3을 보자. 저기 그려져 있는 모든 간선에 대해서 Update를 해줘야하는데 진짜 어림도 없는 방법이 아닐 수 없다. 이걸 parameter마다 해준다? 진짜 어림도 없는 소리가 된다.

그렇다면 다음으로 패기 넘치는 잼민이가 다음과 같이 말한다.

그냥 간단한 함수만 쓰고 손으로 계산하면 안됨? 그것도 못하누 ㅋㅋ루삥뽕

^^ 열심히 해보십셔 잼민님^^(말도 안되는 소리는 집어 치우자)

여기서 tensorflow의 자동 미분(Autograd)가 나오는데, 우리는 이 전에 수학적인 부분으로 이를 접근해 보도록하자.

가장 먼저, 이는 엄청나게 곂곂이 쌓인 함수이다. 일변수 Scalar 함수로 예시를 들어보면 다음과 비슷한 것이라고 생각할 수 있다.

$$y = f(f(f( \cdots f(x) \cdots)))$$

이를 미분해야한다고 생각해보자. Calculus를 배웠다면 가장 먼저 떠오르는 것은 Chain Rule 일 것이다.

하지만, 어디서부터 어떻게 Chain Rule을 적용해야하는지 막막하다. 그 전에 우선 상대적으로 구히기 쉬울 것 같은 출력층 바로 이전의 가중치의 미분을 Chaine Rule을 통해서 구해보자.

$$\frac{\partial E}{\partial w^K_{ij}} = \frac{\partial E}{\partial y_i}\frac{\partial y_i}{\partial u^K_i}\frac{\partial u^K_i}{\partial w^K_{ij}} \tag{Equation (6)}$$

이는 출력층 바로 이전의 층의 가중치이기에, Chain Rule을 통해서 비교적 쉽게 구할 수 있다. 다음과 같이 말이다.
(Error function(목적 함수)는 MSE를 사용하였다고 생각하자.)

$$\frac{\partial E}{\partial y_i} = \frac{1}{N}(y_i - t_i) \quad \frac{\partial y_i}{\partial u^K_i} = f'(u^K_i) \quad \frac{\partial u^K_i}{\partial w^K_{ij}} = z^{K-1}_j \tag{Equation (7)}$$ $$\therefore \frac{\partial E}{\partial w^K_{ij}} = \frac{1}{N}(y_i - t_i)f'(u^K_i)z^{K-1}_j \tag{Equation (8)}$$

이렇게 성공적으로 $W^K$의 미분은 구했다고 치고, 어떻게 그 뒤의 층을 구할 것인가?
우선, 다음 그림을 보자.

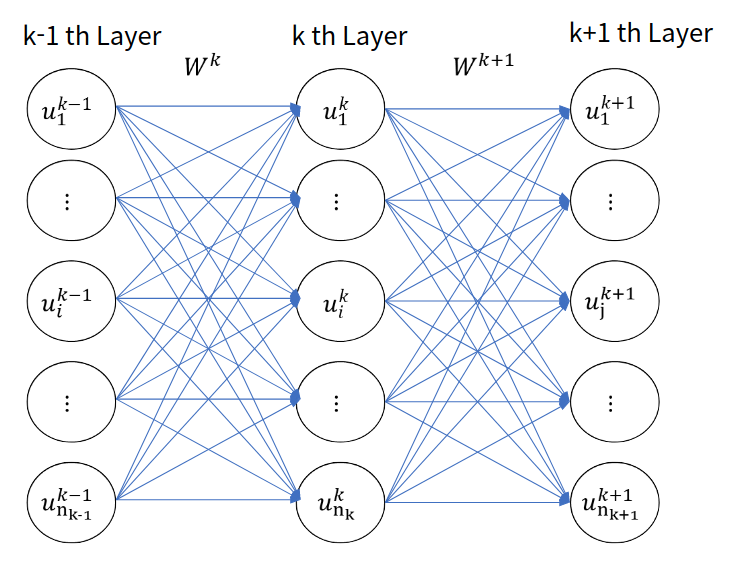
Figure 7. Neural Network 구조에서 일부를 떼어서 표현한 그림
이는 Neural Network 구조에서 일부를 떼어낸 것을 표현한 그림이다. 위의 $\vdots$가 그려진 Unit은 그냥 거기에 많은 수의 Unit들이 있다고 생각하면 될 것이다.
우리는 여기서 $W^k$의 $E$에 대한 미분을 구하는 것이 목표이다.
즉, $Equation (9)$를 구하는 것이 목표이다.

$$\frac{\partial E}{\partial w^k_{ip}} \space = \space ?$$

그것을 위해서 우선, Chaine Rule을 진행해 보자.

$$\frac{\partial E}{\partial w^k_{ip}} = \frac{\partial E}{\partial u^k_i}\frac{\partial u^k_i}{\partial w^k_{ip}} \tag{Equation (9)}$$

여기까지만 봐서는 잘 모르겠다. 하지만 다음의 그림을 보고, $\frac{\partial E}{\partial u^k_i}$ 에 한번 더 Chain Rule을 적용해 보자.

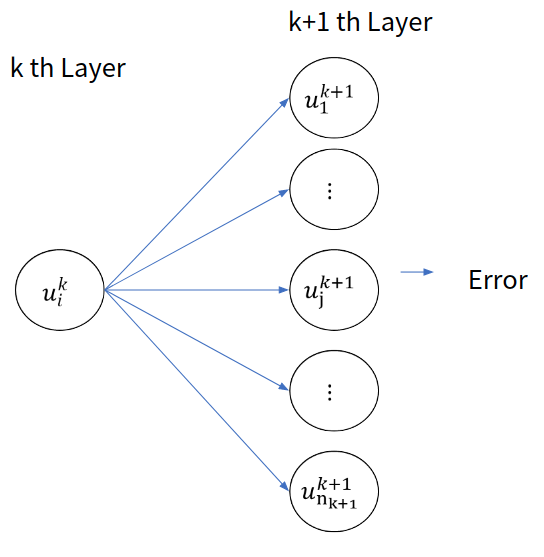
Figure 6. $u^k_i$가 영향을 주는 앞 층의 Unit들
FCNN의 정의에 의해, $u^k_i$는 앞층의 모든 뉴런에 연결되어 있다. 그리고 그 앞 층의 뉴런들은 또 그 다음층으로 값을 전달하며, 점점 출력층에 가까워 지고, Error에 영향을 미치게 된다. 한마디로, 다음과 같이 Chain Rule을 펼칠 수 있다.

$$\frac{\partial E}{\partial u^k_i} = \sum_{j=1}^{n_{k+1}} \frac{\partial E}{\partial u^{k+1}_j}\frac{\partial u^{k+1}_j}{\partial u^k_i} \tag{Equation (10)}$$

이때 우리는 위의 $Equation (10)$에서 유사한 부분을 찾을 수 있다.

$$\frac{\partial E}{\partial u^k_i} \quad and \quad \frac{\partial E}{\partial u^{k+1}_j}$$

그렇다면 우리는 다음과 같이 정의를 해보자.

$$\delta^k_i = \frac{\partial E}{\partial u^k_i} \tag{Def. 8}$$

그렇다면 $Equation (10)$을 다음과 같이 작성할 수 있다.

$$\delta^k_i = \sum_{j=1}^{n_{k+1}} \delta^{k+1}_j\frac{\partial u^{k+1}_j}{\partial u^k_i} \tag{Equation (11)}$$

이 점화식이 이번 포스트의 핵심이다.
그렇다면 식을 다시 정리해서, 최종적인 미분 값을 구해보자.

$$\frac{\partial u^{k+1}_j}{\partial u^k_i} = \frac{\partial u^{k+1}_j}{\partial z^k_i}\frac{\partial z^{k}_i}{\partial u^k_i} = w^{k+1}_{ji}f'(u^k_i) \tag{Equation (12)}$$

그리고, $Equation (12)$를 통해서 $Equation (10)$을 다시 써보면 다음과 같다.

$$\delta^k_i = \sum_{j=1}^{n_{k+1}} \delta^{k+1}_jw^{k+1}_{ji}f'(u^k_i) \tag{Equation (13)}$$

자! 다 왔다. 이제 최종 미분식을 다시 써보자.

$$\frac{\partial E}{\partial w^k_{ip}} = \delta^k_i\frac{\partial u^k_i}{\partial w^k_{ip}} = \left(\sum_{j=1}^{n_{k+1}} \delta^{k+1}_jw^{k+1}_{ji}f'(u^k_i)\right )\frac{\partial u^k_i}{\partial w^k_{ip}}$$ $$\therefore \frac{\partial E}{\partial w^k_{ip}} = \left(\sum_{j=1}^{n_{k+1}} \delta^{k+1}_jw^{k+1}_{ji}f'(u^k_i)\right )z^{k-1}_p \tag{Equation (14)}$$

이 포스트의 핵심은 이것이다.
결국 우리는 상대적으로 구하기 쉬운 출력층의 미분을 구하는 과정에서 미분을 구하기 어려운 층의 미분을 구할 수 있는 실마리를 얻은 것이다.
무슨 말이냐? 우리는 $\delta^k_i$를 정의했다면, 출력층의 $\delta^K$도 구할 수 있을 것이다. 그렇다면 $K-1$층의 $\delta^{K-1}$는 $\delta^K$를 통해서 구할 수 있으니, 결국 $W^{K-1}$층의 미분도 구할 수 있다는 뜻이 된다.

본격적으로 $\delta^K$를 구해보자.

$$\delta^K_i = \frac{\partial E}{\partial y_i}\frac{\partial y_i}{\partial u^K_i} = \frac{1}{N}(y_i - t_i)f'(u^K_i)$$

그렇다. 바로 구할 수 있다. 그렇다면 이를 통해서 뒤에 있는 층의 미분을 차례로 구할 수 있는 것이다.
Feed Forward와는 달리, 이 과정은 방향이 반대로 진행된다. 따라서 이는 Back Propagation이라고 하며, 이렇게 $\delta$를 정의하여 미분을 구하는 방식을 일반화된 델타 규칙이라고 한다.

자, Weight의 미분은 구했으니, Bias의 미분도 구해야한다. 이는 매우 간단하다.

$$\frac{\partial E}{\partial b^k_i} = \frac{\partial E}{\partial u^k_i}\frac{\partial u^k_i}{\partial b^k_i} = \delta^k_i\cdot 1 \tag{Equation (15)}$$

이렇게 우리는 $\delta$에 관한 값만 구하면 신경망을 Update 하기 위한 미분을 전부 구할 수 있다. 그렇기에, 핵심이라고 할 수 있는 방정식 $Def. 8$, $Equation (13)$, $Equation (15)$, $Equation (14)$에 대해서 행렬로써 표현해 보자.

Definition of Delta

$$\Delta^k = \nabla_UE = \nabla_ZE \odot f'(U^k) \tag{Def. 8}$$

Delta Matrix Relation

$$\Delta^k = \left( (W^{k+1})^T\Delta^k \right) \odot f'(U^k) \tag{Equation (13)}$$

Bias Update Equation

$$\nabla_B E = \Delta^k \tag{Equation (15)}$$

Weight Update Equation

$$\nabla_WE = \Delta^kZ^{k-1} \tag{Equation (14)}$$

이걸로 FCNN의 Feed Forward, Back Propagation의 이론적인 부분이 끝났다. 이제 실습은 Part. B에서 마저 다룰 예정이다.