Transformer 강의 내용 part.A

본 포스트는 해당 링크의 블로그을 참조하여 작성되었음을 알립니다.

Index

Attention!
- Seq2Seq
- Attention in Seq2Seq
Transformer Encoder
- Attention in Transformer
- Multi-Head Attention
- Masking
- Feed Forward
Transformer Decoder
Positional Encoding
Partice
- Seq2Seq Attention
- Transformer

여기서는 1은 Part. A이고 2~4는 Part. B에서, 5는 part. C에서 다루도록 하겠다.

Attention!

Seq2Seq

자~ 주목! ㅋㅋㅋ;;
우선 몇몇 사람들은 의아해 할 것이다. 순서상으로는 다음과 같이 가는 것이 국룰이기 때문이다.

RNN -> LSTM -> (GRU) -> Seq2Seq -> Attention

흠… 일단 필자가 생각하기에는 LSTM과 GRU는 RNN에서 구조를 바꾼 것이다. 그리고 이들끼리는 언제나 서로 바뀔 수 있는, 마치 기계 공장의 나사와 같은 존재이기에, 기본이 되는 RNN만을 다루고 넘어간 것이다. 물론! Gradient 입장에서 말한다면 할 말은 많다. 이들이 나온 이론적인 토대는 명확하지만, 굳이? 이걸? 필자의 블로그에서? 다루기에는 너무 흔해 빠진 내용이라 바로 Attention 부터 죠지고 가도록 하겠다. (물론 Attention 또한 요즘은 흔해 빠진 내용 맞다 ㅋ;;)

그래서 왜 Attention에 part 하나를 다 써먹나? 얼마나 중요한 내용이길래?

중요한 내용인 것도 맞지만, 필자가 더 자세히 공부하려고 이런 것이다. 그리고 필자는 이 이후 포스팅에서는 일반화된 델타 규칙을 내세우지 않을 것이다. 왜냐하면 이제부터는 진짜 의미가 없다고 생각하기 때문이다. 이걸 굳이 일반화된 델타 규칙으로 풀어서 구현할 바에는 그냥 AutoGrad를 직접 구현하는게 빠르다.

우선 그렇다면 Attention이 왜 나왔나부터 생각해 보도록 하자.
그러기 위해서는 우선 Seq2Seq부터 알아야 하는데, 간단하게만 알아보도록 하자. 다음 그림으로 Seq2Seq의 구조를 파악할 수 있다.

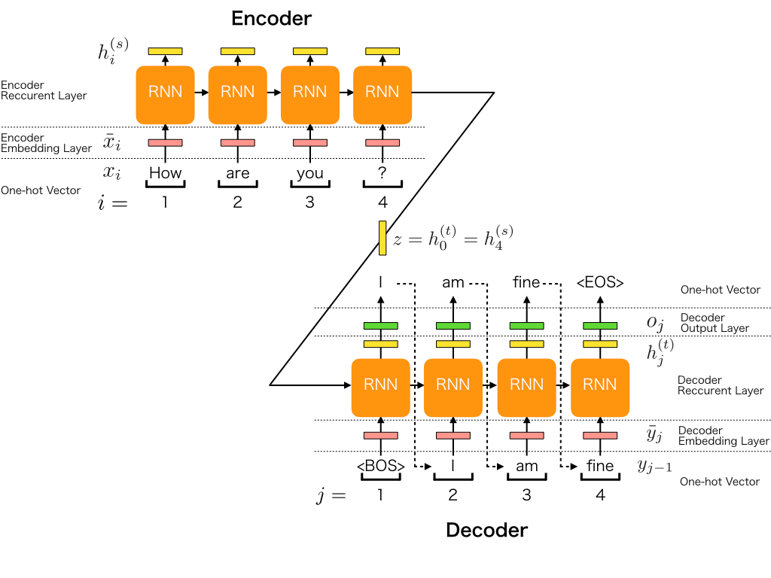
이 Seq2Seq는 그림과 같이 동작한다.
Encoder에서는 입력 벡터의 분석을, Decoder에서는 출력을 결정하는 역할을 한다. 여기서 Encoder는 입력의 Context를 분석하는 역할을 한다고 한다.

Seq2Seq의 단점

입력을 Encoder에서 고정된 크기로 압축하여 context vector로 만든다. 그런 구조는 정보 손실을 가져오기 마련이다.
이러한 Context Vector는 Encoder의 마지막 출력인데 이것만을 사용하게 된다면 초반의 정보는 유실되기 마련이다.
RNN의 고질적인 문제인 Gradient Vanishing 문제가 발생한다.

이를 보완하기 위해서 나온 것이 Attention 구조이다.

Attention in Seq2Seq

먼저, Attention의 큰 구조 부터 알고 넘어가자. Attention은 다음과 같은 함수로 표현될 수 있다.

Attention($Q$, $K$, $V$) = Attention Value

그렇다면 우리는 Attention 함수 자체에 대해서 알기 전에 먼저 $Q$, $K$, $V$를 먼저 정의할 필요가 있다.
Seq2Seq 모델에서 $Q$, $K$, $V$는 다음과 같이 정의될 수 있다.

$Q$ : 특정 시점의 디코더 셀에서의 은닉 상태
$K$ : 모든 시점의 인코더 셀의 은닉 상태들
$V$ : 모든 시점의 인코더 셀의 은닉 상태들

Seq2Seq 모델에서 순전파를 한다면 위의 행렬들을 전부 구할 수 있을 것이다. 그렇다면 우리는 Attention 연산을 정의할 수 있어야 한다. Attention 연산은 되게 다양한 종류가 있다. 간단하게 정리해보자면 다음과 같다.

Dot Attention
Scaled Dot Attention
Bahdanau Attention

우리는 이 중에서 Scaled Dot Attention을 다뤄볼 것이다. 왜냐? Transformer에 쓰이니깐.

Scaled Dot Attention의 수식을 써보자면 다음과 같이 간단하게 쓸 수 있다.

$\text{Attention}(Q, K, V) = \text{Softmax}(\frac{QK^T}{\sqrt{n}})V \tag{definition 1}$

여기서 $n$은 RNN(LSTM이든 뭐든)의 출력 벡터의 크기이다. 즉, $Q$의 크기와 같다.
결국 Attention 구조는 다음과 같은 형식을 띄고 Seq2Seq와 결합한다.

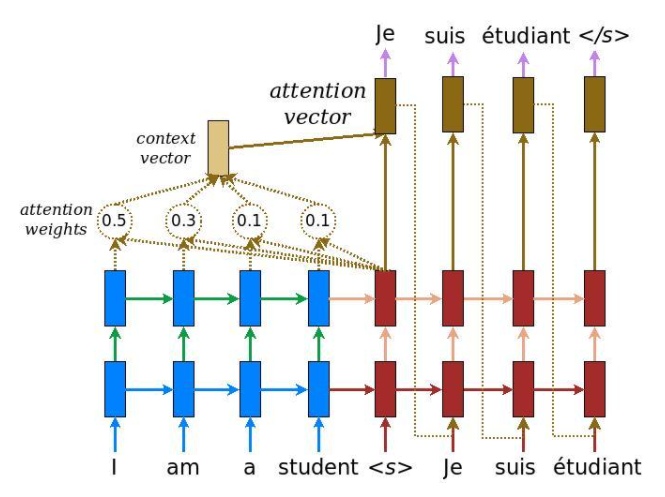
출처: Luong’s paper

위 그림에서 볼 수 있듯이, 각 $Q$ 벡터들은 RNN(또는 LSTM 또는 GRU)의 Decoder 부분의 은닉 상태이다. 각 시간 스텝에서의 출력을 바탕으로 위의 Attention 함수를 Encoder의 출력 값과 같이 계산할 수 있고, 그를 이용해서 Attention Vector를 만들고 다시 $Q$와 결합한 것을 FCNN에 입력하여 최종 출력 vector를 얻어낸 뒤에 Softmax를 씌워서 예측 단어를 분류한다.

말로 길게 설명하였는데, 이를 수식으로 표현해 보자.

$Q^t \in \mathbb{R}^n \\ K \in \mathbb{R}^{n * T} \\ V \in \mathbb{R}^{T * n} \tag{definition 2}$

우선 각 행렬들의 크기는 위와 같이 표현이 가능하다. $Q^t$는 Decoder에서 time step $t$에서의 출력이다. 여기까지 이해가 되었으면 다시 Scaled Dot Attention의 정의에서 성분별로 하나씩 뜯어서 살펴보자.

$Q^tK^{\textbf{T}}$: $K$의 경우, input의 각 time step의 출력을 한데 모아놓은 Matrix이다. 이를 $Q^t$ 벡터와 곱한다. 이를 앞으로 편의상 $e^t$라고 정의하도록 하겠다.
$\text{Softmax}$: 위의 $e^t$에 $\sqrt{n}$로 나눈 값을 Softmax에 집어 넣으므로써 Attention Distribution을 뽑아낸다. 이를 편의상 $\alpha^t$라고 부르도록 하겠다.
$V$: 위의 $\alpha^t$는 $\mathbb{R}^{T}$인 벡터이다. 이 벡터의 각 성분으로 Input Encoder의 각 출력을 가중합한다. 이 결과를 Context vector라고도 부른다.

이렇게 Context Vector를 얻은 후에 우리는 $Q^t$와 Context vector를 Concatenation한 뒤에 FCNN Layer에 입력으로 넣는다.

$W_c \in \mathbb{R}^{n * 2n}: \text{FCNN의 가중치 벡터} \tag{definition 3}$

Context vector와 $Q^t$를 concatenation한 vector의 크기가 $2n$이니, FCNN의 가중치 벡터가 위와 같이 정의되어야 한다.
그리고 그 결과 출력을 Softmax 함수에 넣으면 timestep $t$의 출력이 된다.

이렇게 Attention을 알아 보았는데 다음 파트에서는 Attention이 어떻게 Transformer에 사용되는지를 알아보도록 하겠다.