SLAM Study Part 1.

SLAM Study - Introduction

이번 포스트에서는 SLAM에 관해서 논의해 볼 것이다. 이 포스트는 다음 글을 바탕으로 제작되었다.

Index

1. SLAM: Problem Definition
   1. Mathematical Basis
   2. Example: SLAM in Landmark Worlds
   3. Taxonomy of the SLAM Problem
2. Three Main SLAM Paragigms
   1. Extended Kalman Filters
   2. Particle Methods
   3. Graph-Based Optimization
   4. Relation of Paradigms
3. Visual RGB-D SLAM

SLAM: Problem Definition

SLAM이란, 이동하는 로봇이 미지의 환경과 noise가 낀 Sensor를 가지고 주변 환경의 Map을 만들면서 자기 자신의 상대적인 위치를 특정하는 알고리즘을 일컫는다. 이러한 알고리즘을 배우기 위해서 이 파트에서는 어떠한 수학적 지식이 필요한지와, 어떤 문제들을 해결해 나가야 하는지를 배우게 된다.

Mathematical Basis

SLAM에서 mobile robot의 궤적은 다음과 같이 정의된다.

2차원 평면에서의 좌표 $(x, y)$와 로봇이 향하고 있는 방향 $\theta$의 3차원 벡터의 Sequence

예를 들어서 $x_t = (x,y,\theta)$ 라고 하자. 그렇다면 이러한 궤적(path)는 다음과 같이 정의된다.

$$X_T = \{x_0, x_1, x_2, \dots , x_T\} \tag{Definition 1}$$

이러한 궤적에서 $T$는 $\infin$가 될 수도 있다.
여기서 Odometry라는 개념이 나온다. 이는 무엇이냐면, “시간에 따른 위치 변화를 측정하기 위하여 Sensor의 데이터를 사용하는 것”이다. 굉장히 포괄적인 개념인데, SLAM을 할때는 반드시 나오는 개념이니 꼭 이해해 두도록 하자.

여기서 우리는 간단하게 Odometry로 $t-1$에서 $t$로의 위치 벡터 $x_t$를 추정할 수 있는 데이터 $u_t$가 있다고 가정하자.

그렇다면 다음의 Sequence $U_T$를 로봇의 상대적인 위치의 motion의 정보라고 할 수 있다.

$$U_T = \{ u_1, u_2, \dots, u_T \} \tag{Definition 2}$$

noise가 없는 motion의 경우, $U_T$와 $x_0$만으로도 충분히 경로를 복원할 수 있을 것이다. 하지만 어림도 없다. $U_T$에는 반드시 noise가 끼워져 있을 수 밖에 없다.

최종적으로 로봇은 주변 환경을 감지할 것이다. LiDAR든지 Camera를 사용해서 말이다. 우리는 $m$을 주변 환경에 대한 진짜 지도라고 앞으로 표시하겠다.
이러한 지도 $m$은 Landmark, object, surface 등등으로 구성되어 있을 것이다. 그리고 $m$은 그들의 location이 될 것이다. 그리고 $m$은 종종 time-invariant하다고 간주된다.

주변의 환경 정보 $m$과 자신의 위치 정보 $x_t$ 사이에서 로봇의 measurements는 정보를 수립하게 된다. 만약에 로봇이 정확하게 1번의 기준 시점에서 1개의 measurement를 얻는다면 우리는 이러한 measurement의 sequence를 다음과 같이 표시할 수 있다.

$$Z_T = \{ z_1, z_2, z_3, \dots, z_T \} \tag{Definition 3}$$

그렇다면 우리는 SLAM을 위의 definition 1,2,3을 사용해서 재차 간략하게 표현할 수 있다.

SLAM은 $U_T$와 $Z_T$를 가지고 주변 환경 $m$과 자신의 위치의 sequence $X_T$를 복원하는 문제이다.

이러한 SLAM 문제를 조금 더 세부적으로 나눠서 여러 문제들이 또 존재한다.
첫번째로, 밑의 확률 분포를 구하는 문제를 full SLAM problem이라고 한다.

$$p(X_T, m | Z_T, U_T) \tag{Definition 4}$$

보이다시피, 이 알고리즘을 데이터를 batch 단위로 처리하게된다. 즉, offline이라는 것이다.

두번째로, 밑의 확률 분포를 구하는 문제를 online SLAM problem이라고 한다.

$$p(x_t,m | Z_t, U_t) \tag{Definition 5}$$

Online SLAM은 로봇의 전체 경로를 복원하는 것보다는 현재의 위치에 초점을 맞추고 있다. 이러한 online알고리즘들은 통상 filters라고 부른다.

이러한 SLAM Problem들을 해결하기 위해서는 2가지의 모델이 추가로 필요하다.

1. Odometry Model $U_T$에 대한 수학적인 model
2. 환경 $m$에서 로봇의 위치가 $x_t$일때, measurment $z_t$에 대한 model

그렇다면 우리는 SLAM에서 다음과 같은 확률 분포를 추측하는 것이 타당하다고 쉽게 알 수 있을 것이다.

$$p(x_t|x_{t-1}, u_t) \tag{Definition 6}$$ $$p(z_t|x_t, m) \tag{Definition 7}$$

위 2가지 확률 분포를 여태까지의 내용을 종합해 보았을때 우리가 필요한 2가지의 모델이라고 할 수 있다.

Example: SLAM in Landmark Worlds

우리는 종종 표현하기 어려운 수학적인 모델을 표현하기 쉽도록 가정을 통해서 constraints를 두는 것을 많이 진행한다.

SLAM에서 가장 흔하게 쓰이는 가정이 바로 환경 $m$을 point-landmarks로 표현하는 것이다.
이를 간략하게 설명하자면, 2D 평면에 점들을 찍어서 Map을 표현하는 것이다. 이렇게 표현하면 점의 갯수를 $N$이라고 했을때 Map을 $2N$ Dimension의 벡터로 표현할 수 있다.

이러한 계파에서는 다음과 같이 가정을 하는 것이 일반적이다.

로봇은 다음 3가지를 감지할 수 있다.

1. landmarks 주변의 상대적인 거리
2. landmarks들의 상대적인 bearing (방위각)
3. landmark들의 identity

위에서 1,2번은 noise가 발생할 수 밖에 없다. 하지만 가장 simple한 케이스로 한정을 한다면 3번은 완벽하게 측정할 수 있다.

만약, 3번을 결정하는 문제로 넘어가면 그건 SLAM의 가장 어려운 문제중 하나로 분류된다.

위 설정을 가지고 noise가 없는 measurement function을 먼저 정의해 보도록 하겠다.

$$z^g_t = h(x_t, m) \tag{Definition 8}$$ $$x^g_t = g(x_{t-1}, u_t) \tag{Definition 9}$$

위의 $z^g_t$, $x^g_t$는 각각 $\mathbb{R}^2$, $\mathbb{R}^3$에 속하는 벡터들로써, noise가 없는 진짜 사물의 landmark point/위치이다.

하지만 우리가 실제로 받는 값은 여기에 Noise가 끼기 마련이다. 따라서 이를 수학적으로 정의하기 위해서 우리는 하나의 예시로써 다음과 같이 $z_t$, $x_t$를 정의해 보자.

$\mathcal{N}$을 Gaussian Distribution이라고 하고 $\mathbf{Q}_t \in \mathbb{R}^{2 \times 2}$, $\mathbf{R}_t \in \mathbb{R}^{3 \times 3}$인 Noise Covariance Matrix 2개가 있다고 가정하자.

그렇다면 $z_t$, $x_t$는 다음과 같이 표현할 수 있다.

$$p(z_t | x_t, m) = \mathcal{N}(z^g_t, \mathbf{Q}_t) \tag{Definition 10}$$ $$p(x_t|x_{t-1}, u_t) = \mathcal{N}(x^g_t, \mathbf{R}_t) \tag{Definition 11}$$

물론, 여태까지의 논의는 솔직히 너무 현실과 동떨어져있다. 하지만 명심해야할 점은 어떠한 SLAM 알고리즘이던, 결국에는 $p(zt | x_t, m)$와 $p(x_t|x{t-1}, u_t)$에 대한 논의가 필요하다는 것이다.

Taxonomy of the SLAM Problem

SLAM이 워낙 포괄적인 문제이다보니, 알고리즘별로 여러 접근 방법이 존재한다. 우리는 그것의 분류법을 여기서 다뤄볼 것이다.

1. Full Batch vs Online

   위에서 다룬 논의이니 넘어가도록 하겠다.

2. Volumetric vs Feature-Based

   Volumetric SLAM에서는 Map 정보가 고화질로 sampling되어 주변 환경을 photo-realistic하게 재구축할 수 있는 상황이다. 상당히 많은 데이터를 다루고 그만큼 연산량도 엄청나다.

   그에 비해서 Feature-Based SLAM은 상대적으로 sparse한 정보를 가지고 SLAM을 진행한다. 이 방법이 조금 더 연산량이 가볍고 효율적이지만, 정확도는 상대적으로 떨어질 수 밖에 없다.

3. Topological vs Metric

   Topological한 Mapping 기법은 location들의 관계를 기초로 하여 정의된다. 그에 반해서 Metric Mapping은 location들의 거리(Metric)에 기반하여 Mapping을 진행한다. 요즘 학계에서는 Topological 기법을 거의 쓰지 않는다.

4. Known vs Unknown Correspondence

   Correspondence 문제는 관측된 것들의 Identity끼리의 관계도를 조사하는 것이다. 몇몇 SLAM 알고리즘들에서 이러한 처리를 추가적으로 진행한다. 이러한 Correspondence를 추정하는 문제는 data association 문제라고도 불리우며 SLAM의 가장 난제중 하나이다.

5. Static vs Dynamic

   Static SLAM은 주변 환경이 시간에 따라 변화하지 않는다는 전제를 가지고 SLAM을 진행한다. Dynamic SLAM은 시간에 따라 환경이 변화할 수 있다는 것을 전제로 SLAM을 진행한다.

6. Small vs Large Uncertainty

   SLAM의 문제는 위치의 uncertainty를 어느 정도로 다룰 수 있는지에 따라서 구분된다. closing loop에 대해서는 이러한 uncertainty가 매우 커지는데, 이 문제를 loop closing problem이라고 한다. 이렇게 loop를 닫는 문제를 푸는 것이 현대 SLAM의 특징이다. 이러한 uncertainty는 GPS같이 자신의 절대 위치를 특정할 수 있으면 조금 감소되어진다.

7. Active vs Passive

   Passive SLAM에서는 다른 개체가 로봇을 조종하게 된다. 그리고 SLAM 알고리즘은 순전히 관측만 한다. 대부분의 SLAM 알고리즘이 이것에 속한다.

   그에 반해서 Active SLAM에서는 로봇이 자체적으로 환경을 조사하면서 정확한 지도를 얻어내게 된다.

8. Single-Robot vs Multi-Robot

   notation 대로, 단일 로봇이냐 다중 로봇이냐이다.

9. Any-Time and Any-Space

   이 문제는 제한된 시간과 computation power를 가진 로봇에서 SLAM을 푸는데 있어서 과거의 방법애 대한 대안이다.

Three Main SLAM Paragigms

이 장에서는 다음 3가지의 알고리즘에 대해서 다루게 된다.

• EKF SLAM
• Particle filters
• Graph-Based Optimization

각각의 특성을 알고리즘별로 알아볼 것이다.

Extended Kalman Filters

역사적으로 Extended Kalman Filters(EKF)는 가장 일찍 나왔다. 아마도 가장 영향력 있는 SLAM 알고리즘이 아닐까 싶다.

간략하게 설명하자면, 로봇이 주어진 환경에서 움직이면서 measurement를 수집하는데, system의 state vector와 covariance vector가 Kalman filter로 계속 update가 되는 방식이다.
즉, 새로운 feature가 발견될때마다 quaderatic하게 covariance의 dimension이 증가하게 된다.

이러한 Kalman filter의 구현은 매우 중요하고도 어려운 주제이다. 또한 마찬가지로 sensing과 world modeling 또한 이에 필요한 주제이다. 이는 해당 링크에서 자세한 내용을 확인할 수 있다.

EKF 알고리즘은 robot의 estimation을 다음과 같은 multivariate Gaussian으로 표현한다.

$$p(x_t, m| Z_t, U_t) = \mathcal{N}(\bf{\mu}_t, \bf{\Sigma}_t) \tag{Definition 12}$$

여기서 고차원의 벡터 $\bf{\mu}_t$는 현재 위치 $x_t$에 대해서 최적의 estimation을 나타낸다. 그리고 $\bf{\Sigma}_t$는 $\bf{\mu}_t$에 대한 평균적인 error이다.

지난번에 다루었던 point-landmark 예시에서는 $\bf{\mu}_t$는 $3 + 2N$차원아고 $\bf{\Sigma}_t$는 $(3+2N) \times (3+2N)$차원인 양의 준 정방 행렬이다.

EKF SLAM의 point-landmark example에서의 유도를 간략히 설명해 보자면 한 시점에서 $g$와 $h$가 Talyor Expansion으로 선형화되고, 그 선형화 된 식에 Kalman Filter를 적용하는 방식이다.
EKF SLAM은 기본적으로 online SLAM으로 분류된다. 밑의 그림이 이를 대략적으로 나타내고 있다.

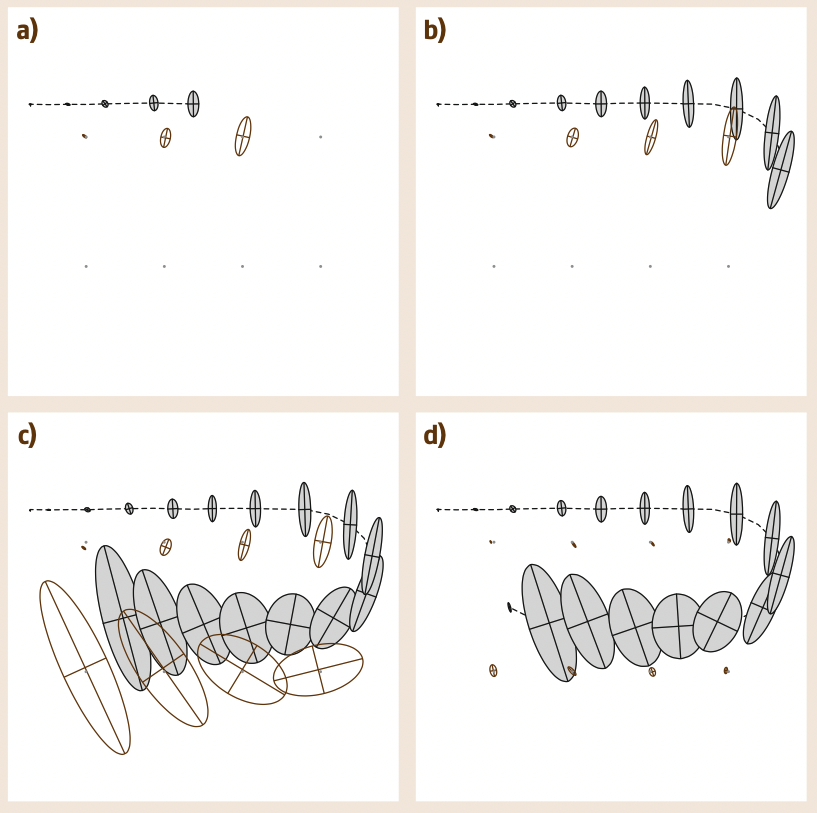
위 그림에서 점선이 로봇의 실제 궤적이고 회색 타원이 EKF가 추정한 로봇의 위치이다. 또한 회색 점이 Landmark point의 실제 위치이고 흰색 타원이 EKF가 추정한 point의 위치이다.

(a-c)까지는 landmark를 마주할 때마다 로봇의 위치의 uncertainty가 커지게 된다. 그리고 (d)에서 로봇이 처음의 landmark를 다시 감지했을때 모든 landmark와 position의 uncertainty가 감소한다. (d를 잘 보면 현재 위치에 대한 uncertainty가 특히 감소되어 있다.)

이러한 현상은 Gaussian Posterior의 Covariance Matrix의 Correlation 덕분이다. 로봇의 위치에 대한 오차가 누적되어 가면서 시간에 따라 추정치는 모호해질 수 밖에 없다. 하지만 상대적으로 잘 알려져 있는 첫번째 landmark의 위치를 확실하게 다시 특정하여 로봇의 위치에 대한 정보를 확정한 순간 연관되어 있는 모든 landmark point에 영향을 주어 정보를 전파할 수 있는 것이다.

EKF SLAM의 가장 기본 전제는 map의 feature들을 로봇이 한 지점에서 완벽하게 관측이 가능하다는 것이다. 물론 아닌 경우에 대한 연구들도 존재한다.
EKF SLAM의 가장 난점은 연산이 quadratic하다는 것이다. 시간 복잡도가 폭팔한다. 이를 해결하기 위해서 EKF의 Extention에 해당하는 연구들이 많이 등장하였는데, 여기서는 다루지 않겠다.

Particle Methods

두번째 방법은 Particle filter를 사용하는 방법이다. 이는 Monte Carlo Method(1947)에 기인하고 있지만, 최근 20년 근처에 꽤 유행하게 되었다.
꽤 추상적으로 먼저 말해보자면, 수 많은 particle들을 모아서 posterior distribution을 추정하는 것이 particle filter 방법이다.

대표적인 알고리즘으로는 Fast SLAM이 있는데, 이를 간략하게 point-landmark example에 대입해서 생각해 보도록 할 것이다.

여기서부터는 Fast SLAM의 설명입니다.

---

모든 시간대에서 FastSLAM은 $K$개의 다음과 같은 type의 Particle을 가진다.

$$X_t^{[k]}, \bf{\mu}_{t, 1}^{[k]}, \dots, \bf{\mu}_{t, N}^{[k]}, \bf{\Sigma}_{t, 1}^{[k]}, \dots, \bf{\Sigma}_{t, N}^{[k]} \tag{Definition 13}$$

위 정의 13에서 $[k]$는 Sample의 index이다. 위 식에 대한 설명을 하자면 다음과 같다.

• Sample Path $X_t^{[k]}$
• $N$ (Landmark의 point의 개수)개의 2-D Gaussian Distribution의 mean $\bf{\mu}{t, n}^{[k]}$과 Covariance Matrix $\bf{\Sigma}{t, n}^{[k]}$

위에서 $n$은 landmark point의 index($1 \leq n \leq N$)이다.

즉, FastSLAM은 $K$개의 Path와 $KN$개의 Gaussian Distribution을 가지고 있는 것이다.
이 파라미터들을 초기화 하는 것은 간단하다. 모든 particle의 로봇의 위치를 원점으로 두고 계산하는 것이다.
그 다음에 parameter의 update는 다음과 같이 수행한다.

1. Odometry의 측정값이 도착하면, 새로운 위치 변수가 각 particle들에 대해서 stochastic하게 생성된다. 이때 location particle들을 생성하는 분포는 definition 14와 같다. 여기서 $x^{[k]}_{t-1}$는 이전 location이며 이러한 확률적 sampling 과정은 kinematics가 계산될 수 있는 어떠한 로봇이든 쉽게 수행될 수 있다.

   $$x^{[k]}_t \approx p(x_t | x^{[k]}_{t-1}, u_t) \tag{Definition 14}$$

2. measurement $z_t$를 받으면 2가지 일이 일어난다.
   첫번째로 각 particle들에 대해서 $z_t$의 확률을 계산한다. definition 15 처럼 말이다.
   이러한 $w_t^{[k]}$를 importance weight라고 한다. (현재 measurement에 대해서 이 particle이 얼마나 중요한지를 나타내는 factor)

   $$w_t^{[k]} = \mathcal{N}(z_t | x^{[k]}_t, \bf{\mu}_{t, 1}^{[k]}, \bf{\Sigma}_{t, N}^{[k]}) \tag{Definition 15}$$

3. 그 다음으로 Fast SLAM은 위에서 만든 importance weight를 가지고 새로운 particle을 뽑는다. 이 과정을 resampling이라고 한다.

4. 그 다음에 새로 뽑은 particle set을 가지고 EKF Filter의 rule에 따라서 parameter를 update 한다.

---

꽤 복잡하게 들리지만, 막상 적용하기는 쉽다.

1. motion sampling은 이미 역학적인 계산으로 쉽게 얻을 수 있고
2. Gaussian measurement를 사용한다면 importance를 계산하는 것도 쉽고,
3. parameter를 update 하는 것도 결국 low-dimension에서 이루어지니 쉽다.

이러한 FastSLAM의 유도 과정에서는 3가지 테크닉을 활용하는데, 간략하게 이름만 적어 보도록 하겠다.

1. Rao–Blackwellization
2. conditional independence
3. resampling

이 3가지 과정을 중점적으로 공부하면서 차후에 FastSLAM은 더 자세히 포스트로 정리해서 올려둘 것이다.

이러한 FastSLAM은 2가지 문제점이 있다.

1. map을 구성하기 위한 sample의 수가 적당히(educated guess) 지정되어야 한다
2. 이전에 mapping된 지역에 재방문 하는 일이 많은 nested loop의 경우에는 particle depletion이 발생할 수 있다.

이를 해결하기 위해서 또 많은 연구들이 등장했는데, 여기서는 다루지 않도록 하겠다.

Graph-Based Optimization

이번에 다룰 내용은 SLAM 문제를 풀 수 있는 3번째 방법인 Graph Based Optimization이다. 이 방법은 non-linear sparse optimization으로 SLAM을 해결한다. 이 방법을 직관적으로 설명하자면 다음과 같다.

1. Landmark와 robot의 location은 graph의 node라고 생각할 수 있다.
2. 각각의 연속된 location pair $x_{t-1}, x_t$는 edge로써 연결되어 있다.
3. 해당 edge는 odometry $u_t$로 부터 나오는 정보를 표현한다.
4. 이때, 해당 edge는 시간 $t$에서의 location $x_t$에서 landmark $m_i$를 감지했을때 발생한다.

이러한 Graph의 Edge는 Soft constraints이다. 이러한 Constraints를 만족시키는 것으로 map과 robot의 full path를 추정할 수 있다. 이 과정은 밑의 그림으로 자세히 설명할 수 있다.

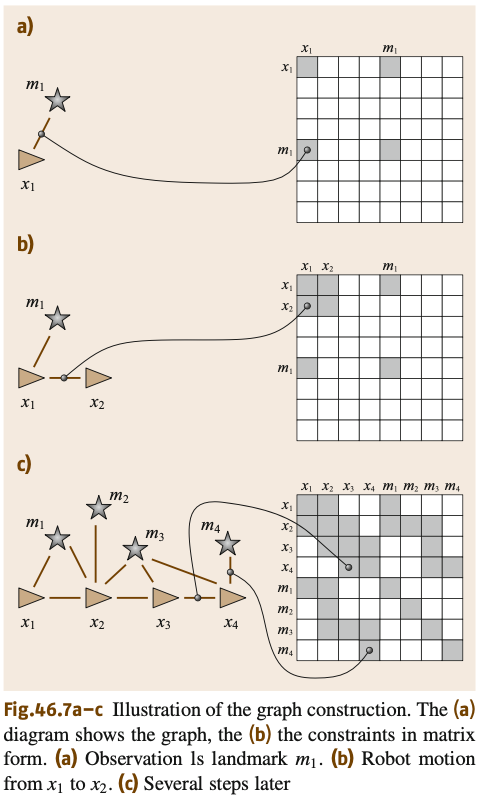
그림을 보면 robot이 이동하면서 위치 $x_t$애서 landmark $m_i$를 감지할때마다 edge가 생기게 되고, 그것을 adjacent matrix로 표현해 나갈 수 있다. 이러한 과정에서 위 matrix는 sparse한 상태로 남게 된다. 최악의 경우에는 node에 비해 constraints의 갯수가 시간과 node의 개수에 대해서 linear해질 수도 있다.

정보 이론적으로 생각해서, 우리가 이러한 SLAM문제를 푸는 것은 이 그래프의 엔트로피를 최소화 하는 것으로 생각해 볼 수 있다. 그 관점에서 우리는 graph를 다루기 이전에 지난번에 정의한 posterior probability에 log를 씌워보자.

$$\ln p(X_T,m |Z_T,U_t) \tag{Definition 16}$$

우리는 각 location과 mapping의 sensing 사건이 독립적이라고 가정했을때 다음과 같이 수식을 전개할 수 있다.

$$\ln p(X_T,m |Z_T,U_t) = \text{const} + \sum_t \log p(x_t | x_{t - 1}, u_t) + \sum_t \log p(z_t | x_t, m) \tag{equation 1}$$

엔트로피를 최소화 한다는 것은 definition 16을 최대화 하는 것과 같다.

$$X_T^*, m^* = \argmax_{X_t, m} \ln p(X_T,m |Z_T,U_t) \tag{equation 2}$$

equation 1을 point-landmark example에서 Gaussian 추정을 적용하여 다음과 같은 quadratic form으로 표현할 수 있다.

$$\ln p(X_T,m |Z_T,U_t) = \text{const} + \\ \sum_t [x_t - g(x_{t - 1}, u_t)]^TR_t^{-1}[x_t - g(x_{t - 1}, u_t)] + \\ \sum_t [z_t - h(x_t, m)]^TQ_t^{-1}[z_t - h(x_t, m)] \tag{equation 3}$$

위 equation 3를 최적화 하는 것이 SLAM문제를 푸는 것으로 연결된다. 흔한 선택지로는 sparse Cholesky & QR decomposition이고, Gradient Descent나 conjugate gradient 방법도 좋은 선택지이다.

Graphical SLAM은 EKF보다 훨씬 더 넓은 map으로 scale을 넓힐 수 있다는 것이 장점이다. 몇몇 추정을 더해야하기는 하지만, EKF에 비하면 Graph method의 update에 필요한 time-complexity와 space-complexity는 각각 constant/linear하다.

Relation of Paradigms

• EKF SLAM: quadratic한 Time/Space Complexity로 인한 map의 scaling에 한계가 있다 + linearization 과정에서 mapping이 잘못될 수 있다.
• Particle filter: EKF SLAM에 있던 계산 복잡도의 한계를 해결했으나, map이 복잡해질 수록 필요한 particle의 수가 기하 급수적으로 늘어난다.
• Graph-based Optimization: 시간복잡도와 공간 복잡도를 혁명적으로 해결함으로써 가장 큰 mapping을 그릴 수 있는 알고리즘이 되었다.

Visual RGB-D SLAM

최근에 SLAM의 중요한 연구 화제는 단영 Visual SLAM이다. Visual SLAM은 RGB-D Sensor(Kinect)나 Camera를 활용하여 주변 map을 생성하거나 로봇의 6-DOF Pose를 추정하는 알고리즘이다. Visual SLAM은 appearance information을 활용해서 loop-closing같은 어려운 문제를 해결할 수 있는 단초를 제공하기도 한다. 이러한 Visual SLAM은 최근까지도 Video Stream을 처리할 HW 성능이 부족해서 난항을 겪고 있었다.
Davison이 이러한 연구에 있어서 선구자적인 역할을 하면서 해당 분야가 각광을 받게 되었다.

Davison과 다른 연구자들에 의하면 Visual SLAM은 camera로 얻어지는 measurement가 odometry 정보를 제공할 수 있게 만드는 것이라고 한다. 이러한 연구들의 종파들 중에는 Feature detection, Feature matching, outlier rejection, constraint estimation, trajectory optimization 등이 있다.

그리고 Visual Information은 loop-closing을 위한 정보 또한 엄청나게 많이 제공을 하는데, 대표적인 예시가 바로 visual object detection을 이용한 location recognition이다.

또한, robust한 visual SLAM의 이정표를 만든 연구는 PTAM이다. 이 연구는 keyframe mapping과 localization을 별도릐 thread로 나눠서 계산을 진행함으로써 online processing에서의 robustness와 성능을 동시에 높일 수 있었다. 여기서의 keyframe은 현재 Visual SLAM에서 복잡도를 줄일 수 있는 방법으로써 주류를 이루고 있다.
다른 방법으로는 view-based mapping system이라고 large-scale에서 pose graph optimization을 기반으로 visual mapping을 진행하는 방법도 있다.

다른 계파로는, RGB-D sensor(Kinect)를 이용해서 mapping과 localization을 동시에 진행하는 연구들도 있다. 그리고 object의 surface를 스캔하는 연구도 있다. 이러한 연구는 sensor의 pose와 surface point의 위치를 최적화 하는 연구이다.

앞으로는 Dense processing method라고 해서 GPU를 활용하여 조금 더 성능을 fine tuning하는 것도 있다.