Mathematical Statistics Chapter 1

Index

1. Introduction
2. What is Set?
3. Probability Set function
4. Conditional Probability and Independency
5. Random Variables
6. Discrete Random Variables
7. Continuous Random Variables
8. Expectation of Random Variable
9. Special Expectation
10. Important Inequality

Introduction

이 카테고리의 글들은 Robert V. Hogg, Joseph W. McKean의 Mathematical Statistics를 정리하는 것이다.
여기서 논의할 수리 통계학에서는 엄밀한 확률론이나 심도 깊은 실 해석학의 내용은 직관적인 설명만으로 퉁치고 넘어갈 예정이다. 더 이상 깊이 파는 내용은 Appendix, 또는 다른 추가적인 포스트로 보충 설명을 하도록 하겠다.
1장의 경우에는 고등학생도 이해할 수 있는 내용만 나오므로 1개의 포스트에 내용을 욱여 넣을 예정이지만, 다른 포스트에서는 그런 일이 없을 것이다.
그리고 주요 예제 및 문제들은 챕터의 마지막 파트의 포스트로 빼서 다룰 것이다.
수리 통계학은 아주 현재 CS의 응용 분야에 빠질 수 없는 내용이다. 따라서 필자도 이 포스트부터는 진지하게 내용을 전개할 것이고 실수, 오타, 기타 틀린 내용은 언제나 About 페이지의 개인 정보로 연락을 주면 고쳐 나가도록 하겠다.

또한, 이 책에서 나오는 예제 R 코드는 전부 Python (with numpy)로 바꿔서 진행할 예정이다. 이유는 필자가 R을 별로 안 좋아하기 때문이다 ㅎㅎ.

마지막으로, 이 글의 예상 독자들은 당연히 고등학교 수학은 다 뗀 사람들이다. 아직 이 조건에 충족하지 못한 사람들은 아쉽지만 고등학교 수학부터 차근 차근 공부하는 것을 추천한다. 너무 낙담하지 말자. 원래 수학은 차근차근 해 나가는 학문이다. 참고로 필자는 00년생이다. 그리고 19년도에 입시를 마쳤다. 그 이후에는 교육 과정이 축소되었다고 알고 있는데, 필자때의 고등 수학을 기준으로 삼을 것이다. (참고로 자랑은 아니지만 필자는 고등학생때 미적분학/선형 대수학을 독학했다. “이거 기준으로 고등 수학을 정의할 것이다”)

What is Set?

우선 확률, 통계를 논하기 전에 가장 기초적인 Mathematical Notation인 Set부터 짚고 넘어갈 필요가 있다.

“집합”이란, 어떤 element의 모임을 설명하는 것이다.

너무 집합에 대해서 복잡하게 생각하지 말자. 집합(Set/Collection)은 어떤 “것”들의 모임이다. 예를 들어, 자연수들의 집합($\mathbb{N}$)같은 것이 있을 수 있고 실수의 집합($\mathbb{R}$)이 있을 수 있다.

이때, 이러한 집합중에서 “셀 수 있는” 원소를 가지고 있는 것을 가산형(countable) 집합 이라고 한다. 유의한 점은 가산형 집합이라는 워딩때문에 해당 집합이 유한한 원소를 가져야만 한다는 것이 아니라는 것이다. 이에 대해서는 나중에 독자들이 꼭 한번 생각해 보는 것을 추천한다.

예를 들어서, 양의 유리수의 집합은 가산형 집합이다. 왜일까?

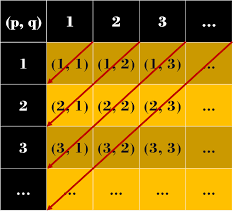
위 그림을 보면 그 답이 나온다. 양의 유리수는 2개의 자연수의 쌍으로 표현할 수 있기 때문에 가산형 집합으로 분류할 수 있다.

이러한 집합 중에서 우리가 봐야할 어떠한 “사건”의 전체에 해당하는 집합을 우리는 표본 집합이라고 부르고 앞으로는 $\mathcal{C}$라고 표현할 것이다. 또한, 어떠한 원소들도 포함하지 않는 집합을 공집합이라고 부르고 $\empty$로 표기할 것이다.
이를 다시 말하면, “사건”은 $\mathcal{C}$의 부분 집합이다. 아주 중요한 개념이지만 해당 내용은 차차 엄밀하게 다루도록 하고 지금은 그렇구나 하고 넘어가면 된다.

이러한 집합을 표현하는데 있어서 Venn Diagram이 유용하게 사용된다. 이는 다음과 같은 집합의 표현 방식중 하나이다.

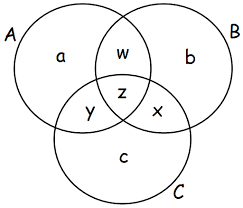
대충 위와 같은 그림이라고 보면 된다. 이에 대한 내용은 이 글을 읽는 독자들은 다 알고 있으리라 추측하고 넘어 가겠다.

집합에도 여러가지 연산이 존재한다. 이 파트에서는 간단하게 어떤 연산들이 있는지를 알아보도록 할 것이다.

우선, 어떤 집합 $A$, $B$가 있다고 가정해보자. 그렇다면 다음의 정의가 성립한다.

1. Complement Set ($A^{\complement}$) : $\mathcal{C}$에서 $A$가 아닌 원소들의 집합을 뜻한다. 즉, $A^{\complement} = {x \in \mathcal{C} | x \notin A}$
2. 집합 $A$의 각 원소가 또한 집합 $B$의 원소이면 집합 $A$는 집합 $B$의 부분 집합이라고 하고 다음과 같이 표현한다. $A \subset B$
3. $A$와 $B$의 합집합이라고 하면 $A$에 있거나 $B$에 있거나 아니면 둘 다에 있는 원소들의 집합이고 다음과 같이 표기한다. $A \cup B$
4. $A$와 $B$의 교집합이라고 하면 $A$와 $B$ 둘 다에 있는 원소들의 집합이고 다음과 같이 표기한다. $A \cap B$
5. 만약, $A \cap B = \empty$이면, $A$와 $B$를 배반 사건이라고 부른다.

이러한 집합의 연산에도 여러가지 연산 규칙이 적용될 수 있다. 대표적으로,

1. 배분 법칙
2. 교환 법칙
3. 드모르간의 법칙

이 있는데, 상세한 내용은 알 것이라고 생각하고 굳이 구구절절 설명은 안 하도록 하겠다. 그 대신 이 부분을 짚고 넘어가자.

$$\bigcup_{n = 1}^{\infty} A_n = A_1 \cup A_2 \cup \dots \tag{definition 1}$$ $$\bigcap_{n = 1}^{\infty} A_n = A_1 \cap A_2 \cap \dots \tag{definition 2}$$

앞으로 이러한 식으로 연속된 집합의 합/교 집합을 표현할 것이다.

이러한 집합열중에는 단조(monotone) 인 집합열도 있는데, 여기에는 2가지 유형이 있다.

1. $n \in \mathbb{N}$에 대하여 $An \subset A{n+1}$ 인 집합열 ${A_n}$을 비감소(nondecreasing) 또는 위로 중첩(nested upper) 라고 한다.
2. $n \in \mathbb{N}$에 대하여 $A_{n+1} \subset A_n$ 인 집합열 ${A_n}$을 비증가(nonincreasing) 또는 아래로 중첩(nested downward) 라고 한다.

이러한 경우에는 다음과 같음이 성립한다.

• 비감소의 경우

$$\lim_{n \rightarrow \infty} A_n = \bigcup_{n = 1}^{\infty} A_n$$

• 비증가의 경우

$$\lim_{n \rightarrow \infty} A_n = \bigcap_{n = 1}^{\infty} A_n$$

다음으로 다룰 개념은 Set을 정의역으로 삼고 실수를 공역으로 삼는 함수이다. 고등학생쯤 된다면 아직 익숙하지 않을 것이다. 자주 다루는 함수는 실수 또는 자연수가 정의역이고 공역이 실수 쯤 될 것이다.
하지만 일단 확률을 이해하는데 있어서 필수불가결인 부분이다. 지금은 받아들이도록 하자.

종종 집합 함수는 합이나 적분으로 정의된다. 다음 (1), (2)는 각각 1,2 차원에서 집합 $A$에 대한 리만 적분을 의미한다.

$$\int_A f(x) dx \tag{1}$$ $$\iint_A g(x, y) dxdy \tag{2}$$

이때 유의해야할 점이 함수 $f$, $g$에 대해서 A를 잘못 설정하게 되면 아예 위 적분이 존재하지 않는 상황이 발생한다는 것이다.

또한, 다음 (3), (4)는 $x \in A$에 대한 $f(x)$의 총합 / $(x,y) \in B$에 대한 $g(x,y)$에 대한 총합을 의미한다.

$$\sum_A f(x) \tag{3}$$ $$\sum_B g(x,y) \tag{4}$$

Probability Set function

이제부터 슬슬 내용이 고등화된다. 우선 어떤 실험이 주어졌을때, 가능한 모든 결과의 표본 공간을 $\mathcal{C}$라고 하자. 일단 그리고 다음과 같은 가정을 추가하겠다.

모든 경우에 사건의 모임이 관심 있는 모든 사건을 포함할 정도로 크고, 여집합의 연산과 가산형 합집합의 연상에 대해 닫혀 있다고 가정한다. 그리고 이러한 사건의 집합을 $\mathcal{B}$라고 표현하자.

전문적으로 이러한 사건의 집합을 $\mathcal{C}$의 부분 집합의 $\sigma$-field라고 한다. 이에 대해서는 추후에 다른 포스트 하나를 소요해서 설명할 예정이다. 진짜 완전 중요한 개념이다.

이제 드디어 확률이 뭔지를 정의할 수 있는 밑밥을 다 깔았다.

$\mathcal{C}$가 표본 공간이고 $\mathcal{B}$가 사건의 집합이라고 하자. 또한, $\mathcal{B}$상에서 정의된 실함수를 $P$라고 하자. $P$가 다음 3가지 조건을 만족하면 $P$를 확률 집합 함수라고 한다.

1. $\forall A \in \mathcal{B}$, $P(A) \geq 0$
2. $P(\mathcal{C}) = 1$
3. 만약, ${A_n}$이 $\mathcal{B}$안에서 사건열이고 모든 $m \neq n$에 대해서 $A_m \cap A_n = \empty$ 일때 다음이 성립한다.

$$P\left( \bigcup_{n = 1}^{\infty} A_n \right) = \sum_{n = 1}^{\infty} P(A_n)$$

조건 3번의 경우에는 원소들이 쌍으로 배반인 사건의 모임을 서로 배타적인 모임이라고 하며 이 모임의 합집합을 배반인 합집합이라고도 한다.
그리고 이러한 합집합이 표본공간이 되면 이 모임을 exhaustive라고 한다.

드디어 확률이 무엇인지 제대로 정의했다. 위 조건을 만족시키는 집합 함수를 우리는 확률이라고 부른다. 아무거나 확률을 가져다 붙이는 것이 아니다.

그리고 이러한 확률은 다음 정리를 만족한다.

1. 각 $A \in \mathcal{B}$에 대하여 $P(A) = 1 - P(A^{\complement})$이다.
2. 공집합의 확률은 0이다.
3. A와 B가 $A \subset B$를 만족하는 사건이면 $P(A) \leq P(B)$이다.
4. 각 $A \in \mathcal{B}$에 대하여 $0 \leq P(A) \leq 1$이다.
5. $A$와 $B$가 $\mathcal{C}$에 있는 사건이면 $P(A \cup B) = P(A) + P(B) - P(A \cap B)$이다.

각 정리에 대한 증명은 책을 참고하자. 굳이 여기서 구구 절절 설명하지는 않겠다.

그리고 여기서 확률 집합 함수의 중요한 정의중 하나인 등가능성 사례를 알아보도록 하겠다.

$\mathcal{C}$가 유한한 표본 공간이라고 하자. 모든 $i = 1,2,…,m$에 대하여 $p_i = 1/m$이고 $\mathcal{C}$이 모든 부분 집합 $A$에 대하여 다음과 같이 정의하자

$$P(A) = \sum_{x_i \in A} \frac{1}{m} = \frac{\#(A)}{m} \tag{definition 3}$$

위 definition 3이 바로 등가능성 사례이다. 이는 매우 흥미로운 확률 모형이다. 주사위, 포커 뽑기 등등 여러 실 사용 예시가 있고 수학적으로 접근하기도 쉽다. 아무래도 그냥 세기만 잘 하면 되기 때문이다.
하지만 이런 것들을 “잘 세는” 것도 매우 중요한 일이다. 이에 대한 좋은 수학적 도구중 대표적으로 순열과 조합이 있다.

1. 순열 (Permutation)

$$P^n_k = n(n - 1)\dotsb(n - k + 1) = \frac{n!}{(n - k)!}$$

1. 조합 (Combination)

$$\binom{n}{k} = \frac{n!}{k!(n - k)!}$$

위 2가지를 모르는 사람은 없을 것이라고 가정하고 넘어 가도록 하겠다.

그리고 이 확률론을 사건열에도 적용하여 또 다른 정리를 끌어낼 수 있다.

1. ${C_n}$을 비감소 사건열이라고 하면 다음이 성립한다.

$$\lim_{n \rightarrow \infty} P(C_n) = P\left( \bigcup_{n = 1}^{\infty} C_n \right)$$

1. ${C_n}$을 비증가 사건열이라고 하면 다음이 성립한다.

$$\lim_{n \rightarrow \infty} P(C_n) = P\left( \bigcap_{n = 1}^{\infty} C_n \right)$$

1. ${C_n}$을 임의의 사건열이라고 하면 다음을 불의 부등식이라 부른다.

$$P\left( \bigcup_{n = 1}^{\infty} C_n \right) \leq \sum_{n = 1}^{\infty} P(C_n)$$

Conditional Probability and Independency

어떤 확률 실험에서는 사건 $A$에만 집중해야하는 경우도 있다. 이렇게 새로운 표본공간 A를 가진 확률 집합함수를 정의하는 문제를 생각해보는 것이 바로 조건부 확률(Conditional Probability)이다. 조건부 확률은 사건 $A$의 가설에 대한 사건 $B$의 확률이 어떻게 정의되는가를 본다. 보통 이러한 확률은 ‘$A$가 주어졌을때(given) $B$의 조건부 확률’이라고 읽고 $P(B|A)$라고 표현한다. 이러한 조건부 확률은 다음과 같이 정의한다.

$$P(B|A) = \frac{P(A \cap B|A)}{P(A|A)} = \frac{P(A \cap B)}{P(A)} \left(\text{where} \space P(A) > 0 \right) \tag{definition 4}$$

그리고 위와 같은 정의로부터 우리는 다음과 같은 결과를 얻을 수 있다.

1. $P(B | A) \geq 0$
2. $P(A|A) = 1$
3. $B1,B_2,\dotsb$가 서로 배타적인 사건일 경우, $P\left(\bigcup{n = 1}^{\infty} Bn | A \right) = \sum{n = 1}^{\infty}P(B_n|A)$

1,2번은 명백하다 그리고 3번에 대한 설명을 추가적으로 하자면 일련의 사건 $B_1,B_2,\dotsb$가 서로 배타적이라고 가정하면 다음이 성립하게 된다.

$$(B_n \cap A) \cap (B_m \cup A) = \empty \left( \text{where} \space n \neq m \right)$$

이를 가산형 합집합에 대한 분배법칙을 활용하면 다음과 같은 결과를 얻을 수 있다.

$$\begin{align*} P\left( \bigcup_{n = 1}^{\infty} B_n \middle| A \right) &= \frac{P\left[ \bigcup_{n = 1}^{\infty} (B_n \cap A) \right]}{P(A)} \\ &= \sum_{n = 1}^{\infty}\frac{P[B_n \cap A]}{P(A)} \\ &= \sum_{n = 1}^{\infty} P[B_n | A] \end{align*}$$

물론, 당연히 여기서 $P(A) > 0$이 성립해야한다.
그리고 조건부 확률의 정의로써 다음을 알 수 있다.

$$P(A \cap B) = P(A)P(B|A)$$

이 관계식을 확률의 곱셈 법칙이라고 한다. 이는 아주 단순하지만 유용하게 사용되고는 한다.
곱셈 법칙은 3개 이상의 사건으로도 확장될 수 있다. 이를 $k$개의 사건으로 확장하는 수학적 귀납법을 활용한 증명을 밑에 적어두도록 하겠다. 나중에 베이즈 정리 등을 이해할때 필수적이닌 꼭 숙지해 두도록 하자.

• $k$개의 사건에 대한 확률의 곱셈 법칙의 증명

---

$P(A_i) > 0, (i = 1,2,\dots,k)$인 $k$개의 배타적이고 전체를 이루는 사건들에 대해서 생각해 보자. 이러한 사건이 $\mathcal{C}$를 분할한다고 여겨도 된다. 이때, 위 확률의 분포가 균일할 필요는 없다. 그리고 $P(B) > 0$인 또 다른 사건 $B$가 있다고 하자. 따라서 사건 $B$는 사건 $A_i, (i = 1,2,\dots,k)$중 단지 하나와 같이 발생한다. 즉,

$$\begin{align*} B &= B \cap \left( \bigcup_{n = 1}^{k} A_n \right) \\ &= \bigcup^{k}_{n = 1}(B \cap A_n) \end{align*}$$

이 성립한다.

이때, $B \cap A_i, (i = 1,2,\dots,k)$는 서로 배반 사건이므로 다음 또한 성립한다.

$$P(B) = \sum_{n = 1}^{k} P(B \cap A_n)$$

이때, $P(B \cap A_i) = P(A_i)P(B | A_i), (i = 1,2,\dots,k)$이므로, 다음이 성립한다.

$$P(B) = \sum_{n = 1}^{k} P(A_n)P(B|A_n)$$

이 결과를 총 확률의 법칙이라고 하고 다음의 매우아주엄청슈퍼중요한 정리로 이어진다.

---

Bayes Theorem

이 파트는 따로 포스트 하나를 떼서 설명해도 모자랄 정도로 매우 중요한 정리이다. 하지만 지금은 가볍게 짚고 넘어가기 위해서 간단한 설명만을 하겠다.

• Bayes Theorem

---

$i = 1,2,\dots,k$에서 $P(A_i) > 0$인 사건들이 있다고 하자. 그리고 이 사건들이 표본공간 $\mathcal{C}$를 분할한다고 가정했을때 $B$가 어떤 사건이라면 다음을 얻을 수 있다.

$$P(A_j | B) = \frac{P(A_j)P(B|A_j)}{\sum_{i = 1}^kP(A_i)P(B|A_i)} \tag{defintion 5}$$

---

이에 대한 증명은 독자들에게 맡긴다. 워낙 쉽기도 하고 위의 총확률의 법칙을 활용하면 되기 때문이다.

여기서 중요한 용어를 조금 정리하고 넘어가고자 한다. 으례 다음과 같이 확률에 이름을 붙이는데, 여러 분야에서 활용되니 알고 넘어가자.

• 위에서 $P(A_i)$를 사전 확률(prior probability)라고 부른다.
• 위에서 $P(A_i|B)$를 사후 확률(posterior probability)라고 부른다.

이에 대한 유용성, 응용 분야는 차례차례 알아가도록 하자. 지금은 일단 알아만 두기를 권장한다.

Independency

어떤 경우에는 사건 $A$에 사건 $B$가 영향을 받지 않는 경우가 있다. 이러한 경우에는 사건 $A$와 $B$는 서로 독립적이다. 라고 부른다.

$$P(B|A) = P(B), (\text{where} \space P(A) > 0)$$

이에 곱셈 법칙을 적용하면 다음과 같은 결과를 얻는다.

$$P(A \cap B) = P(A)P(B)$$

따라서 위의 위의 결과를 만족시키면 사건 $A$, $B$를 서로 독립이라고 불러도 된다.
이를 $k$개의 사건에도 적용할 수 있다. 이 부분에 대한 증명은 독자들에게 맡기도록 하겠다.

Random Variables

이제 독자들은 표본공간 $\mathcal{C}$의 원소가 수가 아닐때는 $\mathcal{C}$를 기술하기가 그렇게 쉽지 않다는 것을 알 수 있을 것이다. 이를 실수로 대응시킬 수 있는 방법이 바로 확률 변수를 사용하는 것이다.

표본공간 $\mathcal{C}$에서 확률 실험이 주어졌다면 각 원소 $c \in \mathcal{C}$에 오직 하나의 실수 $X(c) = x$를 대응시키는 함수 $X$를 확률 변수, random variable이라고 한다. $X$의 공간/범위는 실수의 집합 $\mathcal{D} = { x: x = X(c), c \in \mathcal{C} }$이다.

여기서 표현한 $\mathcal{D}$가 가산형 집합이냐 실수의 구간이냐에 따라서 확률 변수가 이산형(discrete)이냐 연속형(continuous)이냐가 결정이 된다.

자, 이제부터 중요한 내용인 Probability Mass Function(PMF), Probability Density Function(PDF), Cumulative distribuiton function(CDF)가 등장하게 된다.

우선, $X$가 유한공간 $\mathcal{D} = {d_1, \dots, d_m}$에서 정의된 경우를 생각해 보자. 이때, 표본공간 $\mathcal{D}$에서 다음과 같은 함수 $p_X(d_i)$를 정의해보자.

$$p_X(d_i) = P[\{ c: X(c) = d_i \}], \space i = 1,\dots,m \tag{defintion 6}$$

이제 여기서 표본공간 $\mathcal{D}$의 사건 $D$의 확률을 다음과 같이 정의할 수 있다.

$$P_X(D) = \sum_{d_i \in D} p_X(d_i), \space D \subset \mathcal{D}$$

이러한 함수 $p_X(d_i)$를 우리는 확률 질량 함수(PMF)라고 한다.

그렇다면, $X$가 연속형일 경우는 어떨까? 표본 공간이 연속형인 경우에는 단 한 지점에서의 확률을 논하는 것이 의미가 없다. 왜냐? 확률적으로 0.00001도 오차 없이 딱 그 지점에서 사건이 발생할 확률은 0에 수렴하기 때문이다. (직관적으로 받아들이자.)
따라서 우리는 연속형 확률 변수에서는 구간을 지정해서 확률을 구해야 한다.

따라서 우리는 구간 $(a,b) \in \mathcal{D}$에 대해 $X$의 유도된 확률 분포 $P_X$가 정의될 수 잇는 함수를 지정할 수 있다.

$$\begin{align*} P_X[(a,b)] &= P[\{ c \in \mathcal{C}: a < X(c) < b \}] \\ &= \int_a^bf_X(x)dx \end{align*} \tag{definition 7}$$

이러한 함수 $f_X(x)$는 다음과 같은 조건을 만족해야 한다.

1. $f_X(x) \geq 0$
2. $\int_{\mathcal{D}} f_X(x)dx = 1$

이러한 함수 $f_X(x)$를 확률 밀도 함수(PDF)라고 한다.

그리고 이산이건, 연속이건 상관 없이 정의되는 함수가 있다. 바로 누적 분포 함수(CDF)이다.
이는 다음과 같이 정의된다.

$$F_X(x) = P_X((-\infty, x]) = P(\{ x \in \mathcal{C}: X(c) \leq x \}) \tag{definition 8}$$

여기서 위 정의 8의 우항은 $P(X \leq x)$라고 간략하게 표현되기도 한다.

이러한 CDF의 성질은 다음과 같이 정리할 수 있다.

• 누적 분포 함수 $F(x)$를 가진 확률 변수가 $X$일때, 다음이 성립한다.
  1. $\forall (a,b) \in \mathbb{R}^2$, $F(a) \leq F(b), a < b$ (비 감소 함수)
  2. $\lim_{x \rightarrow -\infty} F(x) = 0$
  3. $\lim_{x \rightarrow \infty} F(x) = 1$
  4. $\lim_{x \downarrow x_0} F(x) = F(x_0)$, $F(x)$는 우 연속 함수
• CDF $F_X$를 가진 확률 변수를 $X$라고 하면 $a < b$에서 $P[a < X \leq b] = F_X(b) - F_X(a)$이다.
• 모든 확률 변수에서 $\forall x \in \mathbb{R}$에 대해 $P[X = x] = FX(x) - F_X(x-)$이다. ($F_X(x-) = \lim{z \uparrow x } F_X(z)$)

위 식들에 대한 증명은 나중에 Chapter 1 Appendix의 다른 포스트에서 다루도록 하겠다.

Discrete Random Variables

이산형 확률 변수는 다음과 같이 정의된다.

확률 변수의 공간이 유한이거나 가산형일 경우인 경우에 이러한 확률 변수를 이산형 확률 변수라고 한다.

공간 $\mathcal{D}$를 가진 이산형 확률 변수를 $X$라고 하자. $X$의 확률 질량 함수는 다음과 같이 정의된다.

$$p_X(x) = P[X = x], \space x \in \mathcal{D} \tag{definition 9}$$

이때, PMF는 다음 2가지 성질을 만족해야한다.

1. $0 \leq p_X(x) \leq 1, x \in \mathcal{D}$
2. $\sum_{x \in \mathcal{D}}p_X(x) = 1$

만약, 이산형 집합 $\mathcal{D}$에서 위 2가지 조건을 만족한자면 이 함수는 한 확률 변수의 분포함수를 유일하게 결정한다는 것을 증명할 수 있다. 하지만 여기서는 다루지 않을 것이다.

그리고 여기서 또 한번 중요한 정의가 나온다. 바로 받침(support)이라는 것이다. 공간 $\mathcal{D}$를 가진 이산형 확률 변수 $X$가 있다고 하자. 위의 CDF의 3번째 성질이 의미하는 바를 다시 톺아보자.

모든 확률 변수에서 $\forall x \in \mathbb{R}$에 대해 $P[X = x] = FX(x) - F_X(x-)$이다. ($F_X(x-) = \lim{z \uparrow x } F_X(z)$)

위 정리와 같이 $F_X(x)$의 불연속성은 질량을 정의한다. 즉, $x$가 $F_X$의 불연속점일때 $P(X=x) > 0$이 된다. 우리는 여기서 이산형 확률 변수의 공간과 양의 확률인 이러한 불연속 점들 사이의 특성을 정의하고자 한다.

이산형 확률 변수 $X$의 받침을 양의 확률인 $K$ 공간의 점이라고 하자. $K$의 받침을 나타내기 위해서 흔히 $\mathcal{S}$를 사용한다. (이때, $\mathcal{S} \subseteq \mathcal{D}$ 이다.)

우리가 여기서 알 수 있는 점은 $x \in \mathcal{S} \rightarrow p_X(x) > 0$과 $x \notin \mathcal{S} \rightarrow p_X(x) = 0$이라는 점이다. 따라서 $x \notin \mathcal{S}$인 $x$에서 $F_X(x)$는 연속이다.

너무 어렵게 말했는가? 누구나 알기 쉽게 말하자면 불연속점의 집합을 $\mathcal{S}$라고 하고 거기에 속하지 않은 부분에서의 확률은 $0$이고 아니면 PMF가 확률을 가진다는 뜻이다.

Transformation

통계를 다루면서 자주 부딧히는 문제중에 하나이다. 확률 변수 $X$가 있으며 그것의 분포를 알고 있을때, 우리는 $X$로 표현되는 확률 변수 $Y = g(X)$의 분포를 알고 싶은 것이다. 이때, $X$가 이산형이라면 어떻게 표현할 수 있는지 그것을 알아보고자 한다.

$X$가 공간 $\mathcal{D}_X$를 가진 이산형 확률 변수라고 하자. 그렇다면 $Y$는 공간 $\mathcal{D}_Y = { g(x): x \in \mathcal{D}_X }$일 것이다.
여기서 우리는 2가지 경우를 생각해볼 수 있다.

1. $g$가 1 대 1 함수이다.

   이런 경우에는 문제가 심플해진다. $Y$의 PMF는 다음과 같이 얻을 수 있다.

$$\begin{align*} P_Y(y) &= P[Y = y] \\ &= P[g(X) = y] \\ &= P[X = g^{-1}(y)] \\ &= p_X(g^{-1}(y)) \end{align*}$$

1. 1이 어림도 없는 경우) 이러한 경우에는 함수의 구간별로 나눠서 각각 1대 1인 상황을 만든 후에 변환을 진행하면 된다. (귀찮은 경우이다.)

Continuous Random Variables

앞선 절에서는 이산형 확률 변수에 대해서 알아 보았으니, 이번에는 연속형 확률 변수에 대해서 알아보도록 하겠다.

확률 변수 $X$의 누적 분포 함수 $F_X(x)$가 $\forall x \in \mathbb{R}$에 대해서 연속이라면 확률 변수 $X$를 연속현 확률 변수라고 부른다.

주의해야할 점이 위 CDF의 정리중에서 3번째이다. 연속형에서는 질량점이 없으므로 어느 점을 꼽든지 간에 $P[X = x] = 0$이다. 대부분 연속형 확률 변수는 절대 연속이다. 즉, 어떤 함수 $f_X(t)$에 대하여

$$F_X(x) = \int_{-\infty}^{x} f_X(t)dt$$

이다. 이러한 $f_X(t)$를 우리는 PDF, 확률 밀도 함수라고 한다. 이러한 확률 밀도 함수는 다음 2가지 조건을 만족해야한다.

1. $f_X(x) \geq 0$
2. $\int^{\infty}_{-\infty}f_X(x)dx = 1$

여기서 중요한 점은 한 함수가 위의 2개의 성질을 만족한다면 그것은 한 연속형 확률 변수의 PDF라는 것이다.

Quantile

여기서 등장하는 개념이 분위수이다.

$0 < p < 1$이라고 하자. 확률 변수 $X$의 분포에서 $p$차 분위수는 $P(X < \xi_p) \leq p$, $P(X \leq \xi_p) \geq p$가 되는 $\xi_p$ 값이다. 이를 $X$의 $100p$번째 백분위수라고 한다.

Transformation

그렇다면 연속형 확률 변수에서의 변환은 어떻게 이루어질까? 다음에 그 방법을 설명해두었다.
우리는 CDF를 활용하면 쉽게 그것을 행할 수 있다.

$X$는 pdf $f_X(x)$를 가진 연속형 확률 변수이고 $Y = g(X)$라고 하자. 여기서 $g(x)$는 1대 1 대응 함수이며 미분 가능한 함수이다. $g$의 역함수를 $x = g^{-1}(y)$라고 표현하며 $\frac{dx}{dy} = \frac{d[g^{-1}(y)]}{dy}$라면 $Y$의 pdf는 다음과 같다.

$$f_Y(y) = f_X(g^{-1}(y))\mid\frac{dx}{dy}\mid$$

여기서 $\frac{dx}{dy} = \frac{d[g^{-1}(y)]}{dy}$를 변환의 야코비안(Jacobian, $J$로 표기한다.)이라고 한다.

Expectation of Random Variable

이 파트에서는 기댓값 연산을 소개한다. 다음 정의를 보자.

만약 $X$가 pdf $f(x)$와 다음이 성립하면 연속형 확률 변수이면

$$\int_{-\infty}^{\infty}|x|f(x)dx < \infty$$

$X$의 기댓값은 다음과 같다.

$$E(X) = \int_{-\infty}^{\infty} xf(x)dx \tag{definition 10}$$

만약 x가 이산형 확률 변수이면 다음이 성립할때

$$\sum_{x} |x|p(x) < \infty$$

$X$의 기댓값은 다음과 같다.

$$E(X) = \sum_{-\infty}^{\infty} xp(x) \tag{definition 10}$$

여기서 $E(X)$는 수학적 기댓값(mathematical expectation), $X$의 기댓값(expected value), $X$의 평균 (mean)이라고들 부른다. 일반적으로 $\mu$라고 표기한다.
이러한 평균은 다음 성질들을 가진다.

1. $X$가 확률 변수이고 어떤 함수 $g$에 대하여 $Y = g(X)$라고 하자.

   a. $X$가 pdf $fX$를 가진 연속형 변수일때, $\int{-\infty}^{\infty}|g(x)|f_X(x)dx < \infty$이면 $Y$의 기대값은 존재하며 다음과 같다.

   $$E(Y) = \int_{-\infty}^{\infty}g(x)f_X(x)dx$$

   b. $X$가 pmf $pX$를 가진 이산형 변수이고 $X$의 받침이 $S_X$라고 하자. 만약 $\sum{x \in S_X}|g(x)|p_X(x) < \infty$이면 $Y$의 기댓값이 존재하며 이 값은 다음과 같다.

   $$E(Y) = \sum_{x \in S_X}g(x)p_X(x)$$

2. $g_1(X)$, $g_2(X)$가 $X$의 함수이고 $g_1(X)$, $g_2(X)$의 기댓값이 존재한다고 가정하자. 그렇다면 상수 $k_1, k_2$에 대해서 $k_1g_1(X) + k_2g_2(X)$의 기댓값이 존재하며 이 값은 다음과 같다.

$$E[k_1g_1(X) + k_2g_2(X)] = k_1E[g_1(x)] + k_2E[g_2(x)]$$

Special Expectation

몇몇 특수한 함수의 기댓값은 확률 변수의 특수한 성질들을 끌어내어 그 특성을 파악하는데 도움을 준다. 이러한 특수한 기댓값들의 종류를 이번 장에서는 다뤄볼 것이다.

1. Variance

   이걸 굳이 설명해야하나 싶지만, 일단 정의만 적어 보겠다.

   $$\sigma^2 = Var(X) = E[(X - \mu)^2]$$

2. Moment Generating Function (MGF)

   어떤 $h > 0$에 대하여 $-h < t < h$일때, $e^{tX}$의 기댓값이 존재하는 확률 변수를 $X$라고 하자. $X$의 적률 생성 함수는 $M(t) = E[e^{tX}]$로 정의된다.

   이러한 적률 생성 함수는 특수한 성질을 가지는데, 그것은 다음과 같다.

   0을 초함하는 개구간에 존재하는 적률 생성 함수 $M_X$와 $M_Y$를 가진 확률 변수를 각각 $X,Y$라고 하자. 임의의 $h > 0$에 대해 $-h < t < h$일때, $M_X(t) = M_Y(t)$인 경우에 한하여 모든 $z \in \mathbb{R}$에 대하여 $F_X(z) = F_Y(z)$이다.

   조금 많이 중요한 성질로는 이러한 MGF를 n차 미분한 결과에 0을 대입한 것을 n차 적률(n-th moment) 이라고 부르고 이는 $E(X^n)$과 같다.

3. Characteristic Function

   이는 적률 함수와 모양새가 비슷한데, 허수 단위를 추가한 것이다.
   $\varphi(t) = E[e^{itX}]$ 로 정의되며 $\varphi(t) = M(it)$가 성립한다.

적률 생성 함수와 특성함수는 각각 PDF의 라플라스 변환/푸리에 변환이다. 따라서 각 함수들은 PDF 별로 유일하다.

Important Inequality

여기서는 알아두면 아주 유용한 부등식을 소개할 것이다. 증명은 나중에 Appendix 포스트에서 몰아서 할 것이니 유의하자. 여기서는 소개만 할 것이다.

1. $X$가 확률 변수이고 $m$은 양의 정수이며 $E[X^m]$이 존재한다고 가정하자. 만약 $k$가 양의 정수이고 $k \leq m$이면 $E[X^k]$가 존재한다.
2. [마르코프 부등식]확률 변수 $X$의 음이 아닌 함수를 $u(X)$라고 하자. $E[u(X)]$가 존재하면 모든 양수 $c$에 대하여 다음이 성립한다.

$$P[u(X) \geq c] \leq \frac{E[u(X)]}{c}$$

1. [체비셰프 부등식]확률 변수 $X$가 유한한 분산을 가진다고 하자. 즉, 1번 부등식에 의해 평균이 존재한다고 하면, $k > 0$에 대해서 다음이 성립한다.

$$\begin{align*} P(|X - \mu| \geq k\sigma) \leq \frac{1}{k^2} \\ P(|X - \mu| < k\sigma) \geq 1 - \frac{1}{k^2} \end{align*}$$

1. [옌센의 부등식] 만약, $\phi$가 개구간 $I$에서 볼록이면 $X$가 받침이 $I$안에 있고 유한 기댓값을 가진 확률 변수라면 다음이 성립한다.

$$\phi[E(X)] \leq E[\phi(X)]$$

만약, $\phi$가 순 볼록이면 부등식 $X$가 상수 확률변수가 아닌 한 엄격하다.