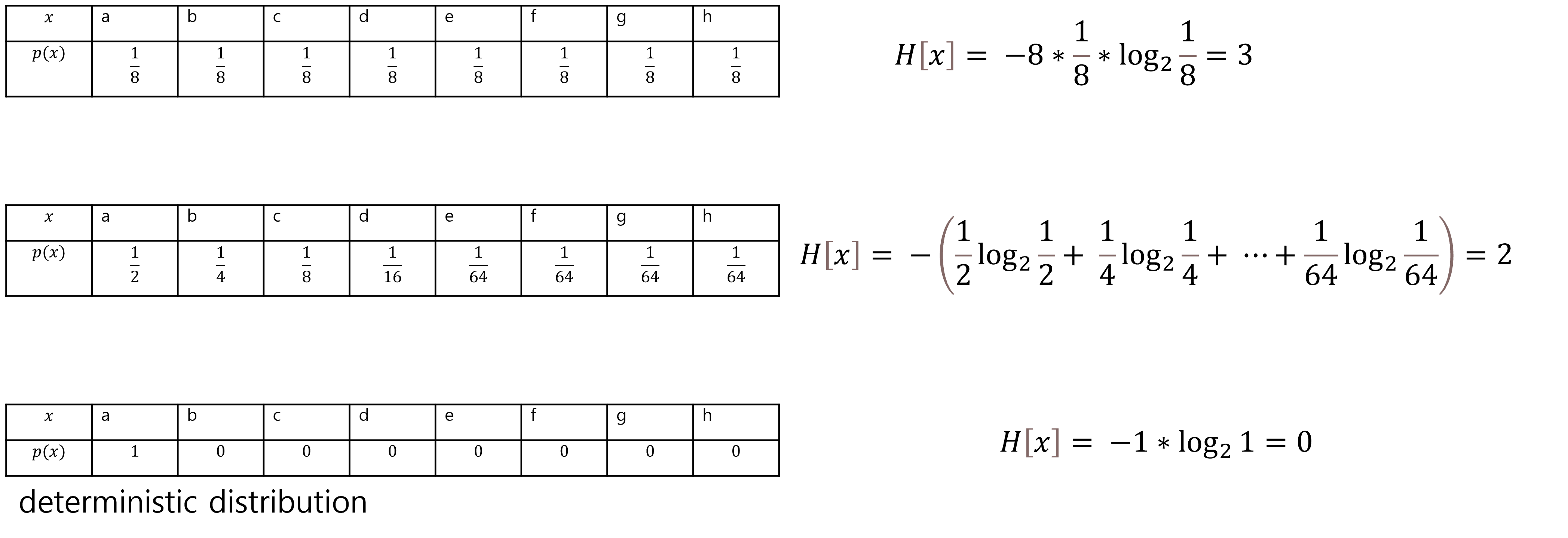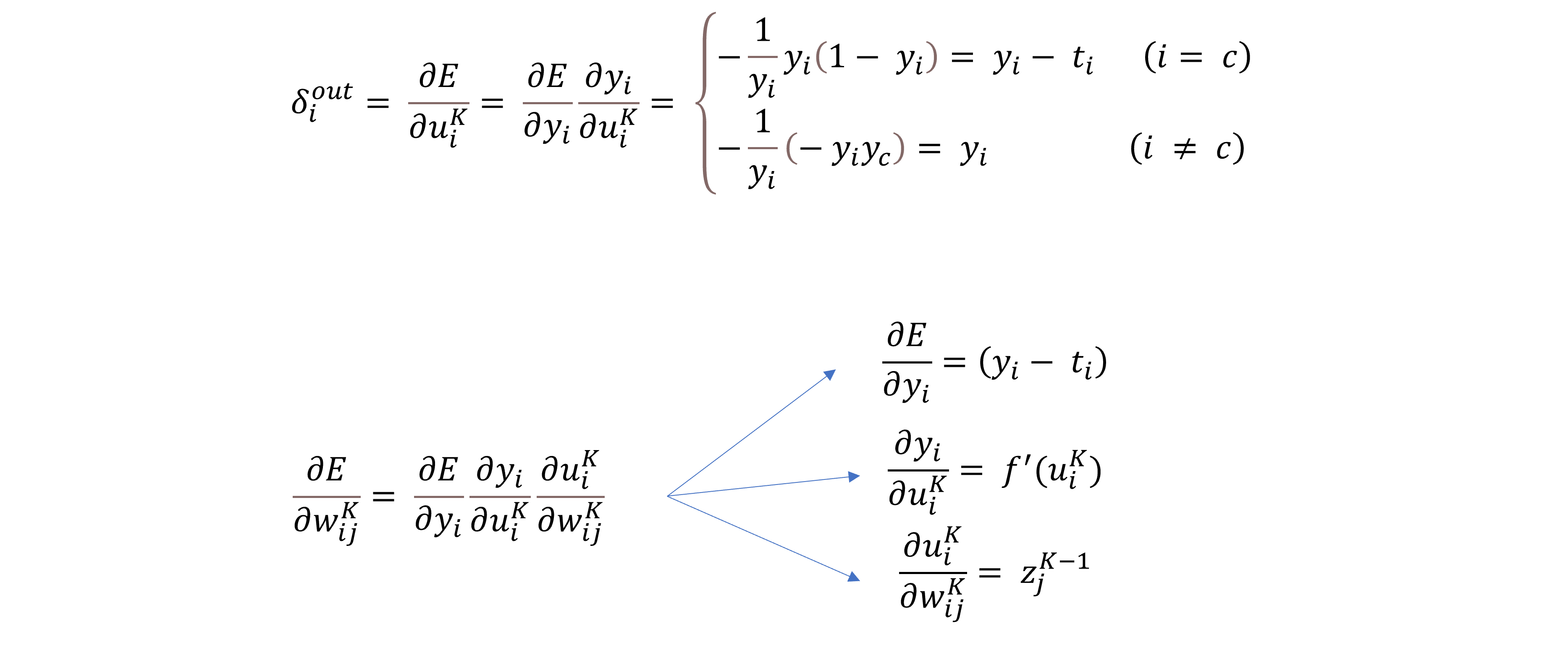Michael's Study Blog

본 포스트는 블로그와논문 “An Image is Worth 16x16 Words: Transformers for iamge recognition at scale”을 참조하여 작성되었음을 알립니다.

Index

1. CNN의 종말
2. Vision Transformer의 구조
3. ViT Inspection
   • Embedding Filters
   • Positional Encoding
   • Attention Distance
4. practice

practice

이제 필자의 Deep learning 포스트도 꽤나 현대적인 수준의 모델을 다루게 되었다. 그리고 이번에는 2019년도에 나온 ViT의 구현이다. ViT의 구현은 생각보다 어렵지 않다. 왜냐면 Transformer의 연장선이기 때문이다. 따라서 기존 Transformer의 부분인 Multi-Head Attention과 Encoder 부분이 아닌 다른 부분만 이 포스트에서 다루도록 하겠다.

먼저, ViT 모델부터 보고 시작하자.

file: model/model.py

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42

class ViT(keras.Model):
    def __init__(self, patch_size, out_dim, mlp_dim, 
                 num_layer, d_model, num_haed, d_ff, drop_out_prob = 0.2):
        super(ViT, self).__init__()
        
        self.d_model = d_model
        self.patch_size = patch_size
        
        self.patch_gen = GeneratePatch(patch_size=patch_size)
        self.linear_proj = keras.layers.Dense(d_model, activation="relu")
        
        self.encoders = [ Encoder(d_model=d_model, num_head=num_haed, d_ff=d_ff, drop_out_prob=drop_out_prob, name = "Encoder_" + str(i + 1)) for i in range(num_layer) ]
        
        self.dense_mlp = keras.layers.Dense(mlp_dim, activation="relu")
        self.dropout = keras.layers.Dropout(drop_out_prob)
        self.dense_out = keras.layers.Dense(out_dim, activation="softmax")
    
    def build(self, x_shape):
        num_patch = (x_shape[1] * x_shape[2]) // (self.patch_size * self.patch_size) 
        
        self.pos_emb = self.add_weight("pos_emb", shape=(1, num_patch + 1, self.d_model))
        self.class_emb = self.add_weight("class_emb", shape=(1, 1, self.d_model)) 

    def call(self, x, training):
        
        patches = self.patch_gen(x)
        x = self.linear_proj(patches)
        
        batch_size = tf.shape(x)[0]
        class_emb = tf.broadcast_to(self.class_emb, [batch_size, 1, self.d_model])    
        x = tf.concat([class_emb, x], axis=1)
        
        x = x + self.pos_emb
        
        for layer in self.encoders:
            x = layer(x, training)
        
        x = self.dense_mlp(x[:, 0, :])
        x = self.dropout(x)
        x = self.dense_out(x)
        
        return x

먼저, 시작 전에 이번에는 다른 모델들과는 사뭇 다르게 build 함수를 overriding해서 사용하였다. 그 이유는 뭐냐? 이전에 ViT의 정의를 보면 명확해 진다.

1. $x_{class}$는 BERT에서 사용되는 것과 똑같은 token이다. 이의 구현 방법은 part.B에서 더욱 자세히 다루어 보도록 하겠다.
2. 각 Image Patch들은 1 개의 FCNN layer를 거치게 된다. 이때, Bias는 없다.
3. 위 표기 중에 $LN$은 Layer Normalization의 약자이다.
4. Encoder를 $L$번 반복하고 나온 결과를 MLP에 넣는다.
5. 최종 결과에 다시 한번 Layer Normalization을 진행한다. 이때, sequence의 마지막 Component만을 가져와서 진행한다.

여기서 논문을 보면 learnable class token $x{class}$라고 나온다. 한마디로 맨 앞에 꼽사리 끼는 $x{class}$ token 또한 학습이 가능한 weight여야 한다는 것이다. 그리고 여기서는 positional encoding 또한 학습이 가능한 weight 여야 한다. 그래서 입력 dimension을 사전에 받아서 모델을 빌드할때 이들을 정의해 줘야한다.

그리고 Image를 Flatten하고 Dense에 넣어줘야 하는데, 이 과정은 다른 layer를 통해서 진행할 것이다. 다음을 보자.

file: model/layer.py

1
2
3
4
5
6
7
8
9
10
11
12
13

class GeneratePatch(keras.layers.Layer):
    def __init__(self, patch_size):
        super(GeneratePatch, self).__init__()
        self.patch_size = patch_size
    
    def call(self, images):
        batch_size = tf.shape(images)[0]
        patches = tf.image.extract_patches(images=images, 
                                        sizes=[1, self.patch_size, self.patch_size, 1], 
                                        strides=[1, self.patch_size, self.patch_size, 1], rates=[1, 1, 1, 1], padding="VALID")
        patch_dims = patches.shape[-1]
        patches = tf.reshape(patches, [batch_size, -1, patch_dims]) #here shape is (batch_size, num_patches, patch_h*patch_w*c) 
        return patches

이 layer를 이용해서 image를 patch로 나눈 뒤에 flatten하고 ViT에서 Dense를 거쳐서 Transformer의 입력으로써 사용한다.
나머지는 Transformer와 같다. 딱히 다를 것이 없다.

본 포스트는 블로그와논문 “An Image is Worth 16x16 Words: Transformers for iamge recognition at scale”을 참조하여 작성되었음을 알립니다.

Index

1. CNN의 종말
2. Vision Transformer의 구조
3. ViT Inspection
   • Embedding Filters
   • Positional Encoding
   • Attention Distance
4. practice

여기서는 1~2은 Part. A이고 3는 Part. B에서 다루도록 하겠다.

CNN의 종말

그렇다. 자연어 처리에서 큰 활약을 보여주던 Transformer는 Vision 영역에도 침범한 것이다. 필자가 이 논문을 처음 보았을때 느꼈던 감정은 아쉬움이었다. 마치 떠나보낸 옛 애인같은 느낌이랄까..? 무슨 헛소리냐 느낄텐데, 고딩학생때부터 필자는 CNN에 미친듯이 시간을 할애하였기에 (필자의 CNN 포스팅 내용은 고딩때 정리한 것을 조금 다듬어서 쓴 것이다. 심지어 그걸 C++로까지 구현했으니 말 다했다 ㅋㅋ;;) 이제 기술의 진보가 내가 가장 아끼던 도구를 구식 취급하는 것이다. 하지만 동시에 온 몸에 전율을 느끼기도 하였다. 시대가 흐른다는 것을 몸소 느끼고 있었기 때문이다.

각설하고, CNN은 Vision 분야에서 Transformer에 비해 다음과 같은 패배 요인이 있다.

“CNN은 공간적인 정보를 Encoding하는데 실패했다.”

이게 머선 소리냐? CNN은 Filter를 학습해서 정보를 습득하였는데, 그것들 간의 연결점이 없다는 것이다. 이를 비유적으로 표현한 그림이 다음과 같다.

위 그림은 CNN의 관점으로 왼쪽이나 오른쪽이나 별반 다를게 없다. 이러한 부분이 CNN이 transformer에 밀리게 되는 요인이 되었다.
이 과정에 대해서는 다다음 파트에서 자세히 알아보도록 하자.

Vision Transformer(ViT)의 구조

우선 논문에서 제시하는 ViT의 구조를 보자.

간단하게 요약하면 다음과 같다.

1. Image를 일정 크기의 Patch로 분할한다.
2. Image를 Flatten하고 FCNN Layer에 거쳐서 일정 크기의 벡터로 만든다.
3. Positional Encoding과 함께 Encoder-Only Transformer에 넣는다.
4. 결과를 MLP에 넣고 Classification한다.

참 쉽죠?

여기까지만 보면 매우 간단하다. 물론 Transformer를 알고 있다는 가정 하에.
따라서 필자도 그렇게까지 자세히 파고 들지는 않고 딱 논문에 나와 있는 수준으로만 구조 분석을 하도록 하겠다. 참고로 이번 포스트 시리즈에서는 딱히 성능 분석은 하지 않고 구조만 분석하고 구현하는 것을 목표로 할 예정이다. 필자는 아직 공부중인 학생이기에 너무 많은걸 목표로 하기 보다는 일단 연산을 똑바로 파악하고 구현하는 것 부터 하는 것이 정도라고 생각한다.

해당 논문에는 매우 친절하게 모델 구조에 대한 수식이 그대로 나와 있다.

앞선 Transformer 포스트를 읽고 왔다면 이해가 한층 쉬울 것이다. 다만 몇가지만 부연 설명을 하고 자세한 것은 part.B에서 다루도록 하겠다.

1. $x_{class}$는 BERT에서 사용되는 것과 똑같은 token이다. 이의 구현 방법은 part.B에서 더욱 자세히 다루어 보도록 하겠다.
2. 각 Image Patch들은 1 개의 FCNN layer를 거치게 된다. 이때, Bias는 없다.
3. 위 표기 중에 $LN$은 Layer Normalization의 약자이다.
4. Encoder를 $L$번 반복하고 나온 결과를 MLP에 넣는다.
5. 최종 결과에 다시 한번 Layer Normalization을 진행한다. 이때, sequence의 마지막 Component만을 가져와서 진행한다.

구조만 놓고 보자면 Transformer만 안다면 전혀 어려운 것이 없다. 다만 구현이 조금 복잡하니 다음 part에서 자세히 다루어 보도록 하자.

ViT Inspection

양산형 블로그답게, 논문에 있는 내용을 한번 정리해 보도록 하겠다. 밑의 사진은 크게 ViT를 3가지 측면으로 분석한 것에 대한 Figure이다.

Embedding Filters

논문의 저자들은 먼저 첫번째로 들어가는 layer에서 Image Patch를 Linear Embedding하는 Dense Weight를 분석해 보았다.
그 결과 위의 맨 왼쪽의 사진처럼 보였다는 내용이다. 하지만 이로써는 그럴듯하게 보이는 기저 함수와 비슷하게 보일 뿐이라고 한다. 필자가 보기에도 이걸로 뭔가를 더 해석하기에는 비약이 너무 심하다고 생각한다.

Positional Encoding

그 후에 논문의 저자들은 Positional Encoding Layer의 Weight를 조사했다. Part.B에서도 다루겠지만, 여기서의 Positional Encoding은 learnable한 weight이다. 이를 시각화 한 것이 위의 사진에서 중간 사진이다. 어떻게 시각화 한 것이냐면, 사진의 각 patch들은 7 7의 크기인데, 해당하는 position의 patch에 대해서 다른 모든 patch들과 cosine similarity를 구한 것이다. 그래서 7 7 크기의 그리드에 사진들이 붙어있는 것이다.
위 그림에 따르면

1. 각자 자기 자신의 위치 근처에서 Cosine Similarity가 높다.
2. 또한 같은 열/행일 수록 유사도가 높다는 것 또한 알 수 있었다.
3. 그리고 가끔씩 큰 그리드에서 측정하면 sin파동 구조가 발생하였다.

그리고 저자들의 추가적인 연구에 의해서 2D Positional Encoding을 수행했을때는 성능의 Improvement가 없었다.

이 4가지 사실을 종합해 보았을때 저자들은 position embedding이 image의 2차원 공간 정보의 형상을 학습할 수 있다고 결론을 지었다.

Attention Distance

Encoder의 Self-Attention 구조는 얕은 층에서도 Image의 전체적인 정보를 통합하게 해준다. (Attention의 구조상 한개의 층에서도 전체적인 정보를 통합시켜주니깐) 저자들은 각 층별로 나온 Attention Distribution를 이용하여 그들을 Weight로 각 Image Patch들의 Pixel 값들의 차이의 평균을 구하였다.
그 결과, 네트워크의 깊이가 깊어질수록 분산은 적어지고 값은 높아지는 것을 확인하였다. 또한 이러한 특성상, 얕은 층의 attention layer들에서 일부 head에 대해서도 높은 attention distance를 보인다. 즉, 얕은 층에서도 전체적인 이미지의 정보를 어느 정도는 통합하고 있었다느 말이 된다.

저자들은 논문 “Quantifying Attention Flow in Transformers
“에 나온 방법을 통해서 Attention score를 input token에 적용하여 계산해본 결과, 꽤나 국지적으로 분류에 의미있는 결과를 얻어낼 수 있었다고 한다. 다음 그림과 같이 말이다.

필자도 얼추 이해만 하고 글을 작성하는 것이라 틀린 부분이 있다면 언제든 지적 부탁한다.

본 포스트는 해당 링크의 블로그와 논문 “Attention is all you need”를 참조하여 작성되었음을 알립니다.

Index

1. Attention!
   • Seq2Seq
   • Attention in Seq2Seq
2. Transformer Encoder
   • Attention in Transformer
   • Multi-Head Attention
   • Masking
   • Feed Forward
3. Transformer Decoder
4. Positional Encoding
5. Partice
   • Seq2Seq Attention
   • Transformer

Partice

이 파트에서는 지난 시간부터 쭉 다뤄온 Attention과 Transformer를 구현해 보는 시간을 가질 것이다. 본격적으로 Model Subclassing API를 제대로 활용하는 시간이 될 것이다.

Seq2Seq Attention

Transformer 구조를 보기 전에 Attention을 Seq2Seq 모델에 적용시켜 보도록 하겠다. 먼저 소스코드부터 보고 가자.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21

class Attention(keras.layers.Layer):
    def __init__(self):
        super(Attention, self).__init__()
        
    def call(self, q, k, v, mask=None):
        # q: (batch_size, seq_len, d_model)
        # k: (batch_size, seq_len, d_model)
        # v: (batch_size, seq_len, d_model)

        matmul_qk = tf.matmul(q, k, transpose_b=True)
        # qk^T : (batch_size, seq_len, seq_len)

        dk = tf.cast(tf.shape(k)[-1], tf.float32)
        scaled_attention_logits = matmul_qk / tf.math.sqrt(dk)
        if mask is not None:
            scaled_attention_logits += (mask * -1e9)
        
        attention_weights = tf.nn.softmax(scaled_attention_logits, axis=-1)
        output = tf.matmul(attention_weights, v)
        # output: (batch_size, seq_len, d_model)
        return output, attention_weights

우선 우리가 사용할 Attention 구조이다. 지난 Transformer part.A에서 정의한 연산(masking 포함)을 고대로 구현한 것이다.
이를 어떻게 Seq2Seq 모델에 적용하는지는 밑의 그림과 소스코드를 보자.

위 그림에 따르면 일단 Seq2Seq는 Encoder와 Decoder가 각기 다른 모델로 있다. 그리고 Encoder에서 나온 모든 time step의 출력과 Decoder의 출력을 같이 사용해서 연산을 해야할 필요가 있다.

필자는 일단 Decoder에 Encoder의 모든 Time step의 출력을 넣는 형식으로 구현을 하였다.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29

class Encoder(keras.Model):
    def __init__(self, WORDS_NUM, emb_dim, hidden_unit, batch_size, *args, **kwargs):
        super().__init__(*args, **kwargs)
        self.batch_size = batch_size
        self.hidden_unit = hidden_unit
        self.embedding = keras.layers.Embedding(WORDS_NUM, emb_dim)
        self.LSTM = keras.layers.LSTM(hidden_unit, return_state=True, return_sequences=True)

    def call(self, inputs, enc_hidden = None):
        x = self.embedding(inputs)
        y, h, _ = self.LSTM(x, initial_state=enc_hidden)
        return y, h

class Decoder(keras.Model):
    def __init__(self, WORDS_NUM, emb_dim, hidden_unit, *args, **kwargs):
        super().__init__(*args, **kwargs)
        self.embedding = keras.layers.Embedding(WORDS_NUM, emb_dim)
        self.lstm = tf.keras.layers.LSTM(hidden_unit, return_sequences=True, return_state=True)
        self.attention = Attention()
        self.dense = tf.keras.layers.Dense(WORDS_NUM, activation='softmax')

    def call(self, x, hidden, mask=None):
        x = self.embedding(x)
        _, h, c = self.lstm(x)
        context_vec, attention_weight = self.attention(h, hidden, hidden, mask=mask)
        
        x_ = tf.concat([context_vec, c], axis=-1)
        out = self.dense(x_)
        return out, h, attention_weight

소스코드를 보기 전에 Attention의 $Q$, $K$, $V$의 정의를 먼저 상기하고 가자.

$Q$ : 특정 시점의 디코더 셀에서의 은닉 상태
$K$ : 모든 시점의 인코더 셀의 은닉 상태들
$V$ : 모든 시점의 인코더 셀의 은닉 상태들

Encoder에서는 Decoder에서 활용하기 위해서 2개의 출력을 내놓는다. 본인의 출력값과 hidden state의 값이다.

Decoder에서는 Encoder에서의 Hidden state를 입력으로 받아서 자신의 hidden state와 같이 attention! 을 진행한다.

이렇게 만들어진 vector와 마지막 출력 값을 concatenation한 값을 dense에 넣어서 최종적인 출력을 내 놓는다.

이의 training loop를 보면 더 이해가 잘 될 것이다.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19

@tf.function
def train_step(inp, targ, enc_hidden):
    loss = 0
    
    with tf.GradientTape() as tape:
        _, enc_hidden = encoder(inp, enc_hidden)
        dec_hidden = enc_hidden
        dec_input = tf.expand_dims([targ_lang.word_index['<start>']] * BATCH_SIZE, 1)
        for t in range(1, targ.shape[1]):
            predictions, dec_hidden, _ = decoder(dec_input, dec_hidden)
            loss += loss_function(targ[:, t], predictions)
            dec_input = tf.expand_dims(targ[:, t], 1)
        
        batch_loss = (loss / int(targ.shape[1]))
        
        variables = encoder.trainable_variables + decoder.trainable_variables
        gradients = tape.gradient(loss, variables)
        optimizer.apply_gradients(zip(gradients, variables))
        return batch_loss

Transformer

이제 대망의 Transformer이다. 먼저 Transformer를 구현하기 위해서 어떤 Component들이 필요했는지 알아보자.

1. Multi-head Attention
2. Positional Encoding
3. Encoder Blocks
4. Decoder Blocks

우리는 이 4가지 Component들을 각각 순차적으로 구현하고 이를 통해서 최종 모델을 구현할 것이다.

file: model/layer.py

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46

class MultiHeadAttention(keras.layers.Layer):
    def __init__(self, d_model, num_head):
        super(MultiHeadAttention, self).__init__()        
        if not d_model % num_head  == 0:
            raise ValueError("Invalid head and d_model!")
        self.d_k = d_model // num_head
        self.num_head = num_head
        self.d_model = d_model
        
        self.Wq = keras.layers.Dense(self.d_model)
        self.Wk = keras.layers.Dense(self.d_model)
        self.Wv = keras.layers.Dense(self.d_model)
        
        self.dense = keras.layers.Dense(self.d_model, activation="relu")

    def split_head(self, batch_size, x):
        x = tf.reshape(x, (batch_size, -1, self.num_head, self.d_k))
        return tf.transpose(x, perm=[0, 2, 1, 3])

    def call(self, q, k, v, mask = None):
        batch_size = q.shape[0]
        
        q, k, v = self.Wq(q), self.Wk(k), self.Wv(v)
        # q: (batch_size, seq_len, d_model)
        # k: (batch_size, seq_len, d_model)
        # v: (batch_size, seq_len, d_model)
        
        q, k, v = self.split_head(batch_size, q), self.split_head(batch_size, k), self.split_head(batch_size, v)
        # q: (batch_size, num_head, seq_len, d_k)
        # k: (batch_size, num_head, seq_len, d_k)
        # v: (batch_size, num_head, seq_len, d_v)
        
        qkT = tf.matmul(q, k, transpose_b=True) # (batch_size, num_head, seq_len, seq_len)
        d_k = tf.cast(self.d_k, dtype=tf.float32)
        scaled_qkT = qkT / tf.math.sqrt(d_k)
        if not mask == None:
            scaled_qkT += (mask * -1e9)
        
        attention_dist = tf.nn.softmax(scaled_qkT, axis=-1)
        attention = tf.matmul(attention_dist, v) # (batch_size, num_head, seq_len, d_k)
        
        attention = tf.transpose(attention, perm=[0, 2, 1, 3]) # (batch_size, seq_len, num_head, d_k)
        concat_attention = tf.reshape(attention, (batch_size, -1, self.d_model)) # (batch_size, seq_len, d_model)
        output = self.dense(concat_attention)
        
        return output

각 연산 뒤에 차원을 적어 두었으니 이해하기는 어렵지 않을 것이다. 구체적인 정의가 떠오르지 않을 독자들을 위해서 Multi-Head Attention의 수식을 적어두고 가겠다.

위 수식을 고대~로 구현한 것 밖에 되지 않는다.

그리고 positional Encoding은 다음과 같이 구현했다.

file: model/layer.py

1
2
3
4
5
6
7
8
9
10
11
12

def get_angles(pos, i, d_model):
    angle_rates = 1 / np.power(10000, (2 * (i//2)) / np.float32(d_model))
    return pos * angle_rates
    
def positional_encoding(position, d_model):
    angle_rads = get_angles(np.arange(position)[:, np.newaxis], np.arange(d_model)[np.newaxis, :], d_model)

    angle_rads[:, 0::2] = np.sin(angle_rads[:, 0::2])
    angle_rads[:, 1::2] = np.cos(angle_rads[:, 1::2])

    pos_encoding = angle_rads[np.newaxis, ...]
    return tf.cast(pos_encoding, dtype=tf.float32)

이것 또한 정의를 고대로 구현한 것이다. (참 쉽죠?)

이제 Encoder와 Decoder Block을 구현할 차례이다. 귀찮으니 한번에 소스를 적어 두도록 하겠다.

file: model/layer.py

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67

class Encoder(keras.layers.Layer):
    def __init__(self, d_model, num_head, d_ff, drop_out_prob = 0.2):
        super(Encoder, self).__init__()
        self.d_model = d_model
        self.num_head = num_head
        
        self.MultiHeadAttention = MultiHeadAttention(d_model=d_model, num_head=num_head)
        
        self.dense_1 = keras.layers.Dense(d_ff, activation="relu")
        self.dense_2 = keras.layers.Dense(d_model, activation="relu")
        
        self.layernorm1 = keras.layers.LayerNormalization(epsilon=1e-6)
        self.layernorm2 = keras.layers.LayerNormalization(epsilon=1e-6)

        self.dropout1 = keras.layers.Dropout(drop_out_prob)
        self.dropout2 = keras.layers.Dropout(drop_out_prob)

    def call(self, x, training=True, mask=None):
        
        out_atten = self.MultiHeadAttention(x, x, x, mask)
        out_atten = self.dropout1(out_atten, training=training)
        x = self.layernorm1(out_atten + x)
        
        out_dense = self.dense_1(x)
        out_dense = self.dense_2(out_dense)
        out_dense = self.dropout2(out_dense, training=training)
        x = self.layernorm2(out_dense + x)
        
        return x
        
    
class Decoder(keras.layers.Layer):
    def __init__(self, d_model, num_head, d_ff, drop_out_prob = 0.2):
        super(Decoder, self).__init__()
        self.d_model = d_model
        self.num_head = num_head
        self.MultiHeadAttention1 = MultiHeadAttention(d_model, num_head)
        self.MultiHeadAttention2 = MultiHeadAttention(d_model, num_head)
        
        self.dense_1 = keras.layers.Dense(d_ff, activation="relu")
        self.dense_2 = keras.layers.Dense(d_model, activation="relu")
        
        self.layernorm1 = tf.keras.layers.LayerNormalization(epsilon=1e-6)
        self.layernorm2 = tf.keras.layers.LayerNormalization(epsilon=1e-6)
        self.layernorm3 = tf.keras.layers.LayerNormalization(epsilon=1e-6)
        self.dropout1 = tf.keras.layers.Dropout(drop_out_prob)
        self.dropout2 = tf.keras.layers.Dropout(drop_out_prob)
        self.dropout3 = tf.keras.layers.Dropout(drop_out_prob)
        
        pass

    def call(self, x, enc_output, training, look_ahead_mask, padding_mask):
        
        out_atten1 = self.MultiHeadAttention1(x, x, x, look_ahead_mask)
        out_atten1 = self.dropout1(out_atten1, training=training)
        x = self.layernorm1(out_atten1 + x)
        
        out_atten2 = self.MultiHeadAttention2(enc_output, enc_output, x, padding_mask)
        out_atten2 = self.dropout2(out_atten2, training=training)
        x = self.layernorm2(out_atten2 + x)
        
        out_dense = self.dense_1(x)
        out_dense = self.dense_2(out_dense)
        out_dense = self.dropout3(out_dense, training=training)
        x = self.layernorm3(out_dense + x)
        
        return x

Encoder는 별로 볼게 없고, Decoder를 보자면 지난번 정의에서 다뤘듯이, 첫번째 Multi-Head Attention과 두번째 Mutli-Head Attention은 다른 입력이 주어지고, 다른 masking이 주어진다.

따라서 Decoder의 입력으로 출력 sequence, encoder 출력, look ahead masking, padding masking이 들어가야 한다.

자세한 정의는 part.B를 다시 참고하자.

참고로, masking은 다음 함수로 만들었다.

file: model/model.py

1
2
3
4
5
6
7
8
9

def create_padding_mask(seq):
    seq = tf.cast(tf.math.equal(seq, 0), tf.float32)
    # add extra dimensions to add the padding
    # to the attention logits.
    return seq[:, tf.newaxis, tf.newaxis, :]  # (batch_size, 1, 1, seq_len)

def create_look_ahead_mask(size):
    mask = 1 - tf.linalg.band_part(tf.ones((size, size)), -1, 0)
    return mask  # (seq_len, seq_len)

그리고 최종적으로 이렇게 만든 Encoder, Decoder Block을 쌓아서 Transformer 모델을 만들어야 한다.

편의상, Encoder모델, Decoder 모델을 만들고 이를 하나로 합쳐서 Transformer 모델을 만들었다.

file: model/model.py

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72

class EncoderModel(keras.Model):
    def __init__(self, input_voc_size, num_layers, max_seq_len, d_model, num_head, d_ff, drop_out_prob = 0.2):
        super(EncoderModel, self).__init__()
        self.d_model = d_model
        self.num_layers = num_layers
        self.embedding = tf.keras.layers.Embedding(input_voc_size, d_model)
        self.pos_encoding = positional_encoding(max_seq_len, self.d_model)
        self.enc_layers = [ Encoder(d_model, num_head, d_ff, drop_out_prob) for _ in range(num_layers) ]
        self.dropout = tf.keras.layers.Dropout(drop_out_prob)
        
    def call(self, x, training, mask):
        
        seq_len = tf.shape(x)[1]
        x = self.embedding(x)
        x += self.pos_encoding[:, :seq_len, :]
        x = self.dropout(x, training=training)
        
        for i in range(self.num_layers):
            x = self.enc_layers[i](x, training, mask)
            
        return x
        
class DecoderModel(keras.Model):
    def __init__(self, output_voc_size, num_layers, max_seq_len, d_model, num_head, d_ff, drop_out_prob = 0.2):
        super(DecoderModel, self).__init__()
        self.d_model = d_model
        self.num_layers = num_layers
        self.embedding = tf.keras.layers.Embedding(output_voc_size, d_model)
        self.pos_encoding = positional_encoding(max_seq_len, self.d_model)
        
        self.dec_layers = [ Decoder(d_model, num_head, d_ff, drop_out_prob) for _ in range(num_layers) ]
        self.dropout = tf.keras.layers.Dropout(drop_out_prob)
        
    def call(self, x, enc_output, training, look_ahead_mask, padding_mask):
        
        seq_len = tf.shape(x)[1]
        x = self.embedding(x)
        x += self.pos_encoding[:, :seq_len, :]
        x = self.dropout(x, training=training)
        
        for i in range(self.num_layers):
            x = self.dec_layers[i](x, enc_output, training, look_ahead_mask, padding_mask)
            
        return x
    
class Transformer(keras.Model):
    def __init__(self, input_voc_size, output_voc_size, num_layers, max_seq_len_in, max_seq_len_out, d_model, num_head, d_ff, drop_out_prob = 0.2):
        super().__init__()
        self.Encoder = EncoderModel(input_voc_size, num_layers, max_seq_len_in, d_model, num_head, d_ff, drop_out_prob)
        self.Decoder = DecoderModel(output_voc_size, num_layers, max_seq_len_out, d_model, num_head, d_ff, drop_out_prob)
        
        self.final_layer = tf.keras.layers.Dense(output_voc_size)
        
    def call(self, inputs, training):
        inp, tar = inputs
        
        enc_padding_mask, look_ahead_mask, dec_padding_mask = self.create_masks(inp, tar)
        enc_output = self.Encoder(inp, training, enc_padding_mask)
        dec_output = self.Decoder(tar, enc_output, training, look_ahead_mask, dec_padding_mask)
        
        final_output = self.final_layer(dec_output)
        return final_output
        
    def create_masks(self, inp, tar):
        enc_padding_mask = create_padding_mask(inp)
        dec_padding_mask = create_padding_mask(inp)

        look_ahead_mask = create_look_ahead_mask(tf.shape(tar)[1])
        dec_target_padding_mask = create_padding_mask(tar)
        look_ahead_mask = tf.maximum(dec_target_padding_mask, look_ahead_mask)

        return enc_padding_mask, look_ahead_mask, dec_padding_mask

그리고 Transformer에서 보면 Embedding layer를 사용하는데, 이는 Dense와 결과적인 측면에서는 다를 것이 없디. 하지만 token을 vector로 Embedding하는데 있어서 훨씬 효율적이니 되도록 token을 vector로 임베딩할때 이걸 사용하도록 하자.

각 Encoder와 Decoder는 num_layer(hyper parameter)만큼 Encoder, Decoder 블록을 반복해서 쌓고, 그것들을 차례로 출력으로 내놓는다. 이제 2개를 합쳐서 간단하게 Transformer 모델이 완성되는 것이다.

이쯤되면 필자들도 느낄 것이다. 이럴때 Model Subclassing API가 빛을 발휘한다. 이 각각의 Component들을 함수로만 구현하는 것 보다는 class로 묶어서 관리하는 것이 가독성, 유지보수 측면에서 훨씬 이득이다.

그리고 논문에 의하면, Transformer는 독자적인 learning rate scheduler를 가진다. 이 수식은 다음과 같다.

이를 구현하기 위해서 다음과 같이 Custom Scheduler를 만들 수 있다.

file: model/model.py

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21

class CustomSchedule(keras.optimizers.schedules.LearningRateSchedule):
    def __init__(self, d_model, warmup_steps=4000):
        super(CustomSchedule, self).__init__()

        self.d_model_save = d_model
        self.d_model = tf.cast(d_model, tf.float32)

        self.warmup_steps = warmup_steps

    def __call__(self, step):
        arg1 = tf.math.rsqrt(step)
        arg2 = step * (self.warmup_steps ** -1.5)

        return tf.math.rsqrt(self.d_model) * tf.math.minimum(arg1, arg2)
    
    def get_config(self):
        config = {
            'd_model': self.d_model_save,
            'warmup_steps': self.warmup_steps,
        }
        return config

여기까지 구현하면 Transformer의 구현은 끝이 난다. 굳이 여기서는 Training loop까지는 다루지 않겠다. 한번 필자가 직접 완성해 보도록 하자. 정 모르겠다면 필자의 github에 완성판이 있으니 직접 가서 찾아 보기를 바란다.

본 포스트는 해당 링크의 블로그와 논문 “Attention is all you need”를 참조하여 작성되었음을 알립니다.

Index

1. Attention!
   • Seq2Seq
   • Attention in Seq2Seq
2. Transformer Encoder
   • Attention in Transformer
   • Multi-Head Attention
   • Masking
   • Feed Forward
3. Transformer Decoder
4. Positional Encoding
5. Partice
   • Seq2Seq Attention
   • Transformer

여기서는 1은 Part. A이고 2~4는 Part. B에서, 5는 part. C에서 다루도록 하겠다.

Transformer Encoder

자 드디어 대망의 Transformer이다. 현대 Deep learning model의 기초라고도 할 수 있을 만큼 많이 쓰이는 모델이므로 블로그 주제에 선정되었다. 이를 위해서 하고 싶지도 않았던 Attention 공부를 해왔는데, 공부하고 보니 보람 넘치는 시간이었던 것 같다.

Attention in Transformer

우선 Transformer를 제시한 논문의 이름이 “Attention is all you need”라는 것을 파악하고 가자. (필자 생각에는 이때부터 살짝 논문 이름이 제목학원이 된 것 같기도 하다.. ㅋㅋ;;) 한마디로, 기존에 Seq2Seq 같은 경우에는 RNN/LSTM/GRU의 보완제로써 Attention을 사용했다면, Transformer에서는 Attention만을 사용하여 신경망을 구성한다.

일단, 양산형 블로그글의 클리셰답게, Transformer의 논문에서 Model Architecture의 모식도를 가져와 봤다. 여기에 들어가는 Component를 하나하나 분해해 보면 다음과 같이 정리할 수 있다.

1. Multi-Head Attention
2. Feed Forward Network
3. Masked Multi-Head Attention
4. Positional Encoding
5. *$N$ ?
6. Residual Connection

우리는 이 모두를 하나하나 분해해서 살펴볼 것이다. (5번인 Residual Connection은 다른 Post에서 집중적으로 다루어 볼 것이다.) 그 전에 먼저 Transformer에서 Attention이 어떻게 정의되고 쓰이는지를 알아볼 것이다. 우선, 우리는 Attention을 정의하려면 먼저 $Q$, $K$, $V$를 정의해야한다는 것을 이전 포스트에서 다루었다.

위 행렬의 크기/정의는 어떤 attention이냐에 따라서 달라진다. 이때 attention의 종류는 이전 포스트에서 언급했던 “누가 만든 attention”이냐가 아니라 어떤 식으로 Attention 연산이 이루어 지냐이다. Transformer에서는 아래의 3가지 타입의 attention이 사용된다.

출처: 위 링크에 나와있는 블로그

위 3가지 attention에 따라서 $Q$, $K$, $V$의 출처가 달라진다.
정리하자면 다음과 같다.

Encoder의 Self Attention : Query = Key = Value
Decoder의 Masked Self Attention : Query = Key = Value
Decoder의 Encoder-Decoder Attention : Query : 디코더 벡터 / Key = Value : 인코더 벡터

자, 이제 어떻게 $Q$, $K$, $V$가 정의되는지 파트별로 나눠놨으니 남은 것은 본격적으로 연산에 들어가는 것이다.

그 전에 Transformer에서 사용되는 Hyper Parameter를 먼저 알아보도록 하겠다.

1. $d_{model}$ = 512: Transformer의 인코더와 디코더의 입력과 출력의 크기를 결정하는 parameter이다.
2. $N$ = 6: Transformer에서 Encoder와 Decoder가 총 몇 개의 층으로 이루어져 있는지를 나타내는 기준이다.
3. $H_n$ = 8: Multi head Attention에서 Attention을 병렬로 수행하고 합치는 방식을 사용하는데, 그때 몇개로 분할할지를 결정하는 hyper parameter이다.
4. $d{ff}$ = 2048: Transformer의 내부에 Feed Forward 신경망이 존재하는데, 이 신경망의 은닉 unit의 개수를 의미함. 물론, 이 layer의 출력은 당연히 $d{model}$ 이 된다.

Multi-Head Attention

또 양산형 블로그 클리셰답게 논문에 있는 Figure를 가지고 왔다.

위 그림을 보면서 설명을 읽으면 이해가 잘 될 수 있도록 글을 구성해 보도록 하겠다.
우선 가장 보편적으로 활용되는 자연어 처리를 예로 들고 싶지만, 필자의 성격상 그런 것 보다는 조금 일반적으로 이야기를 하도록 하겠다. 어떤 연속열 데이터 $x1, x_2, x_3 …x_n$ 이 있다고 가정해 보자. 이들 각각이 $x_i \in \mathbb{R}^{d{model}}$ 인 벡터라고 해보자. 자연어 처리라면 Word Embedding으로 생성된 단어 벡터라고 할 수 있고 설령 다른 문제더라도 이것과 비슷하게 representation이 가능하다면 뭐든 학습이 가능하다는 것이다. 이러한 input을 활용해서 $Q$,$K$,$V$를 얻어 보도록 하자.

우리는 3개의 FCNN Layer를 활용해서 입력으로부터 $Q$,$K$,$V$를 얻어낼 것이다.
다음과 같이 FCNN Layer의 Weight를 정의해 보도록 하겠다.

여기서 $dk = d_v = d{model}/H_n$이다. 그리고 sequence length를 $n$이라고 가정하자. 그렇다면 우리는 결과로써 나오는 각 $Q$,$K$,$V$ 행렬의 결과의 크기를 다음과 같다고 생각할 수 있다. 그리고 여기서 $i$는 $1 \leq i \leq H_n$이다. 나중에 각 i별로 병렬로 계산하고 Concatenation을 진행하는 과정을 거칠 것이다. 그래서 Multi Head Attention이다.

이 상태에서 지난 포스트에서 주로 다뤘던 Scaled Dot Attention에 대해서 다시 한번 상기하고, 적용해 보자.

이 Attention의 결과 행렬을 $O_i$라고 했을때, $O_i \in \mathbb{R}^{n * d_v}$이다.
이제 각기 계산한 $O_i$들에 대해서 concatenation을 진행한다. 그 후에 다시 한번 FCNN Layer에 통과시키게 된다.

그렇다면 결과적으로는 다음이 성립한다.

여기까지가 Encoder에 적용시킬 Multi Head Self Attention 이다.

Masking

Masking은 Sequential한 데이터에서 쓸데없는 데이터까지 학습되지 않도록, 또는 원하는 방향으로 데이터를 학습시킬 수 있게 해주는 좋은 도구이다. Transformer에서는 $Q_iK_i^T$룰 계산하면서 나오는 $\mathbb{R}^{n*n}$ 행렬에 적용시키게 된다. 몇가지 예시를 들면서 설명해 보도록 하겠다.

1. padding의 학습을 막기 위한 용도 (Padding Mask)

sequence의 길이를 통일시키기 위해, 길이가 모자란 데이터에는 으례 padding을 넣게 된다. 하지만 padding은 실질적인 의미를 가진 데이터가 아니기에 학습에서 배제를 해야한다. 그래서 우리는 $Q_iK_i^T$의 행렬에서 Softmax 함수를 거치기 전에 $-\inf$ 값을 곱하므로써 Attention Distribution에서 Padding에 해댱하는 위치의 값을 0으로 만들어 버린다. 학습에서 배제를 시키는 것이다.

해설이 어렵다면 다음 그림을 보자.

1. 자신보다 앞의 데이터를 학습하지 않게 하는 용도

이 Masking은 Decoder에서 사용된다. $Q_iK_i^T$ 행렬에서 자기 자신보다 앞서 있는 데이터를 참조하는 현상이 일어난다. 이는 Transformer가 데이터를 순차적으로 받는 것이 아닌, 한번에 받기 때문에 그런 것이다. 이 문제를 해결하기 위해서 $Q_iK_i^T$ 행렬에 자신보다 앞선 값에는 $-\inf$를 곱해서 Attention Distribution의 값을 0으로 만들어 버린다.

이것도 해석이 어렵다면 다음 그림을 보자.

이를 look ahead masking 이라고 한다.

Feed Forward

Transformer에서는 다음과 같은 형태의 FCNN Layer 2개를 겹쳐서 Encoder/Decoder에 사용하고 있다.

위 2개의 $W$행렬은 각 FCNN layer의 가중치 행렬의 크기이다. 이 2개의 FCNN Layer에 사이에 ReLU activation function을 끼워 넣어서 사용한다.

Transformer Decoder

자, 이제 Decoder에 대한 이야기를 해볼 것이다. 하지만 여기까지 읽었다면 Decoder를 굳이 다뤄야 할지도 의문일 정도로 유추하기 쉬워졌다.

Decoder와 Encoder가 다른 점은 위 그림에서 있는 것이 전부이다.

1. 첫번째 Multi Head Attention에서 Look Ahead Masking을 사용했다는점
2. 2번째 Multi Head Attention에서 Encoder의 Output을 Key와 Value 행렬로써 사용 한다는점

Residual Connection 특성상, 같은 차원으로 입/출력 행렬이 일괄되기 때문에 위화감 없이 전개가 가능할 것이다. 이 부분은 독자에게 어떤 식으로 연산이 이루어지는지 생각할 시간을 가져보는 것을 추천한다.

Positional Encoding

마자믹으로 Positional Encoding에 대해서 알아볼 것이다. Positional Encoding은 입력의 데이터의 위치 정보를 신경망에 알려주는 한가지의 수단이다. 이것이 필요한 이유는 다양하다. 대표적으로 NLP에서는 어순 또한 언어의 뜻을 이해하는데 중요한 정보이기 때문이다.

대표적인 몇가지 예시를 들자면 다음과 같다.

1. Simple Indexing

이는 단순하게 입력이 들어온 순서대로 0, 1, 2, 3, … 의 값을 할당하여 Embedding Layer 같은 것을 거쳐서 벡터로 만드는 방법이다. 가장 단순하지만 딱히 추천하지는 않는다고 한다.

1. Sin 함수를 이용한 Positional Encoding

이는 position에 따라서 다음과 같은 수식으로 계산되는 값을 사용하는 방법이다.

이때, $pos$는 Sequence 내에서 입력의 위치를 나타내며, $i$는 Embedding vector 내에서의 위치를 나타낸다.

자세한 것은 다음 그림을 보면 더 자세히 알 수 있다.

이걸로 기나긴 Transformer의 이야기는 끝났다. 다음 포스팅은 이것을 구현해 보는 시간을 가질 것이다.

본 포스트는 해당 링크의 블로그을 참조하여 작성되었음을 알립니다.

Index

1. Attention!
   • Seq2Seq
   • Attention in Seq2Seq
2. Transformer Encoder
   • Attention in Transformer
   • Multi-Head Attention
   • Masking
   • Feed Forward
3. Transformer Decoder
4. Positional Encoding
5. Partice
   • Seq2Seq Attention
   • Transformer

여기서는 1은 Part. A이고 2~4는 Part. B에서, 5는 part. C에서 다루도록 하겠다.

Attention!

Seq2Seq

자~ 주목! ㅋㅋㅋ;;
우선 몇몇 사람들은 의아해 할 것이다. 순서상으로는 다음과 같이 가는 것이 국룰이기 때문이다.

RNN -> LSTM -> (GRU) -> Seq2Seq -> Attention

흠… 일단 필자가 생각하기에는 LSTM과 GRU는 RNN에서 구조를 바꾼 것이다. 그리고 이들끼리는 언제나 서로 바뀔 수 있는, 마치 기계 공장의 나사와 같은 존재이기에, 기본이 되는 RNN만을 다루고 넘어간 것이다. 물론! Gradient 입장에서 말한다면 할 말은 많다. 이들이 나온 이론적인 토대는 명확하지만, 굳이? 이걸? 필자의 블로그에서? 다루기에는 너무 흔해 빠진 내용이라 바로 Attention 부터 죠지고 가도록 하겠다. (물론 Attention 또한 요즘은 흔해 빠진 내용 맞다 ㅋ;;)

그래서 왜 Attention에 part 하나를 다 써먹나? 얼마나 중요한 내용이길래?

중요한 내용인 것도 맞지만, 필자가 더 자세히 공부하려고 이런 것이다. 그리고 필자는 이 이후 포스팅에서는 일반화된 델타 규칙을 내세우지 않을 것이다. 왜냐하면 이제부터는 진짜 의미가 없다고 생각하기 때문이다. 이걸 굳이 일반화된 델타 규칙으로 풀어서 구현할 바에는 그냥 AutoGrad를 직접 구현하는게 빠르다.

우선 그렇다면 Attention이 왜 나왔나부터 생각해 보도록 하자.
그러기 위해서는 우선 Seq2Seq부터 알아야 하는데, 간단하게만 알아보도록 하자. 다음 그림으로 Seq2Seq의 구조를 파악할 수 있다.

이 Seq2Seq는 그림과 같이 동작한다.
Encoder에서는 입력 벡터의 분석을, Decoder에서는 출력을 결정하는 역할을 한다. 여기서 Encoder는 입력의 Context를 분석하는 역할을 한다고 한다.

Seq2Seq의 단점

1. 입력을 Encoder에서 고정된 크기로 압축하여 context vector로 만든다. 그런 구조는 정보 손실을 가져오기 마련이다.
2. 이러한 Context Vector는 Encoder의 마지막 출력인데 이것만을 사용하게 된다면 초반의 정보는 유실되기 마련이다.
3. RNN의 고질적인 문제인 Gradient Vanishing 문제가 발생한다.

이를 보완하기 위해서 나온 것이 Attention 구조이다.

Attention in Seq2Seq

먼저, Attention의 큰 구조 부터 알고 넘어가자. Attention은 다음과 같은 함수로 표현될 수 있다.

Attention($Q$, $K$, $V$) = Attention Value

그렇다면 우리는 Attention 함수 자체에 대해서 알기 전에 먼저 $Q$, $K$, $V$를 먼저 정의할 필요가 있다.
Seq2Seq 모델에서 $Q$, $K$, $V$는 다음과 같이 정의될 수 있다.

$Q$ : 특정 시점의 디코더 셀에서의 은닉 상태
$K$ : 모든 시점의 인코더 셀의 은닉 상태들
$V$ : 모든 시점의 인코더 셀의 은닉 상태들

Seq2Seq 모델에서 순전파를 한다면 위의 행렬들을 전부 구할 수 있을 것이다. 그렇다면 우리는 Attention 연산을 정의할 수 있어야 한다. Attention 연산은 되게 다양한 종류가 있다. 간단하게 정리해보자면 다음과 같다.

1. Dot Attention
2. Scaled Dot Attention
3. Bahdanau Attention

우리는 이 중에서 Scaled Dot Attention을 다뤄볼 것이다. 왜냐? Transformer에 쓰이니깐.

Scaled Dot Attention의 수식을 써보자면 다음과 같이 간단하게 쓸 수 있다.

여기서 $n$은 RNN(LSTM이든 뭐든)의 출력 벡터의 크기이다. 즉, $Q$의 크기와 같다.
결국 Attention 구조는 다음과 같은 형식을 띄고 Seq2Seq와 결합한다.

출처: Luong’s paper

위 그림에서 볼 수 있듯이, 각 $Q$ 벡터들은 RNN(또는 LSTM 또는 GRU)의 Decoder 부분의 은닉 상태이다. 각 시간 스텝에서의 출력을 바탕으로 위의 Attention 함수를 Encoder의 출력 값과 같이 계산할 수 있고, 그를 이용해서 Attention Vector를 만들고 다시 $Q$와 결합한 것을 FCNN에 입력하여 최종 출력 vector를 얻어낸 뒤에 Softmax를 씌워서 예측 단어를 분류한다.

말로 길게 설명하였는데, 이를 수식으로 표현해 보자.

우선 각 행렬들의 크기는 위와 같이 표현이 가능하다. $Q^t$는 Decoder에서 time step $t$에서의 출력이다. 여기까지 이해가 되었으면 다시 Scaled Dot Attention의 정의에서 성분별로 하나씩 뜯어서 살펴보자.

1. $Q^tK^{\textbf{T}}$: $K$의 경우, input의 각 time step의 출력을 한데 모아놓은 Matrix이다. 이를 $Q^t$ 벡터와 곱한다. 이를 앞으로 편의상 $e^t$라고 정의하도록 하겠다.
2. $\text{Softmax}$: 위의 $e^t$에 $\sqrt{n}$로 나눈 값을 Softmax에 집어 넣으므로써 Attention Distribution을 뽑아낸다. 이를 편의상 $\alpha^t$라고 부르도록 하겠다.
3. $V$: 위의 $\alpha^t$는 $\mathbb{R}^{T}$인 벡터이다. 이 벡터의 각 성분으로 Input Encoder의 각 출력을 가중합한다. 이 결과를 Context vector라고도 부른다.

이렇게 Context Vector를 얻은 후에 우리는 $Q^t$와 Context vector를 Concatenation한 뒤에 FCNN Layer에 입력으로 넣는다.

Context vector와 $Q^t$를 concatenation한 vector의 크기가 $2n$이니, FCNN의 가중치 벡터가 위와 같이 정의되어야 한다.
그리고 그 결과 출력을 Softmax 함수에 넣으면 timestep $t$의 출력이 된다.

이렇게 Attention을 알아 보았는데 다음 파트에서는 Attention이 어떻게 Transformer에 사용되는지를 알아보도록 하겠다.

본 포스트는 Hands-on Machine learning 2nd Edition, CS231n, Tensorflow 공식 document, Pattern Recognition and Machine Learning, Deep learning(Ian Goodfellow 저)을 참조하여 작성되었음을 알립니다.

Index

1. Essential Mathematics
   • Basic of Bayesian Statistics
   • Information Theory
   • Gradient
2. Loss Function Examples
3. What is Optimizer?
4. Optimizer examples
5. Partice

Partice

자, 이제 구현의 난이도 측면에서는 가장 어렵다고 말할 수 있는 파트가 왔다. 이번에도 Model Subclassing API를 활용하여 Custom Optimizer를 만들어 보도록 하겠다. Custom이라고 해서 뭔가 새로운건 아니고, 간단하게 SGD를 구현해 볼 것이다. 근데 솔직히 이건 별로 쓸데가 없다. 이것까지 건드려야하는 사람은 아마도 직접 짜는게 빠르지 않을까 싶다.
여기서 가장 중요한 것은 Custom Training loop와 Custom loss이다. SGD는 간단하게 소스코드만 보고 Training loop와 Custom loss를 자세히 설명하도록 하겠다.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44

class CustomSGDOptimizer(keras.optimizers.Optimizer):
    def __init__(self, learning_rate = 0.001, name = "CustomSGDOptimizer", **kwargs):
        super().__init__(name, **kwargs)
        self._set_hyper("learning_rate", kwargs.get("lr", learning_rate))
        self._is_first = True

    def _create_slots(self, var_list):
        for var in var_list:
            self.add_slot(var, "pv") # previous variable
        for vat in var_list:
            self.add_slot(var, "pg") # previous gradient
    
    @tf.function
    def _resource_apply_dense(self, grad, var):
        var_dtype = var.dtype.base_dtype
        lr_t = self._decayed_lr(var_dtype)

        new_var_m = var - lr_t * grad

        pv_var = self.get_slot(var, "pv")
        pg_var = self.get_slot(var, "pg")

        if self._is_first :
            self._is_first = False
            new_var = new_var_m
        else:
            cond = grad * pg_var >= 0
            avg_weight = (pv_var + var) / 2.0
            new_var = tf.where(cond, new_var_m, avg_weight)
        
        pv_var.assign(var)
        pg_var.assign(grad)

        var.assign(new_var)

    def _resource_apply_sparse(self, grad, var):
        raise NotImplementedError
    
    def get_config(self):
        base_config = super().get_config()
        return {
            **base_config,
            "learning_rate" : self._serialize_hyperparameter("lr")
        }

그만 알아보자.

장난 안치고 이건 나중에 하나의 포스트를 다 써서 설명할 것이다. 그 정도로 다른 중요한 topic과 같이 다루기에는 무겁다.

일단, Custom Training loop를 어떻게 만드는지를 알아보도록 하겠다.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43

train_dataset = tf.data.Dataset.from_tensor_slices((train_img, train_labels))
                            # 섞어.                        # 배치 사이즈 만큼 나눠.
train_dataset = train_dataset.shuffle(buffer_size=1024).batch(BatchSize)

# Optimizer & Loss Function 정의
optimizer = keras.optimizers.Adam(learning_rate=LR)
loss_function = keras.losses.SparseCategoricalCrossentropy(from_logits=True)

train_accuracy = keras.metrics.SparseCategoricalAccuracy()
val_acc_metric = keras.metrics.SparseCategoricalAccuracy()

for epoch in range(EPOCHS):
    print("Epoch %d start"%epoch)
    # step, 1개의 batch ==> 의사 코드에서 batch 뽑는 역할
    for step, (x_batch, y_batch) in enumerate(train_dataset):
        # **********************************************************************************************
        with tf.GradientTape() as tape:
            logits = model(x_batch, training=True)
            loss_val = loss_function(y_batch, logits)
            # 여기서 신경망의 Feed Forward & Expectation of Loss 계산을 진행함.
        # tape.gradient를 호출하면 ==> gradient 계산이 진행됨.
        grad = tape.gradient(loss_val, model.trainable_weights)
        # 정의된 Optimizer를 이용해서 Update를 진행함.
        optimizer.apply_gradients(zip(grad, model.trainable_weights))

        # train에서의 정확도를 계산함.
        train_accuracy.update_state(y_batch, logits)
        if step % 500 == 0 :
            print("Training loss at step %d: %.4f"%(step, loss_val))
    
    # 정확도 뽑아 보겠다.
    train_acc = train_accuracy.result()
    print("Training acc over epoch: %.4f" % (float(train_acc),))
    train_accuracy.reset_states()

    for x_batch_val, y_batch_val in validation_dataset:
        val_logits = model(x_batch_val, training = False)
        val_acc_metric.update_state(y_batch_val, val_logits)
    val_acc = val_acc_metric.result()
    print("Validation acc: %.4f" % (float(val_acc),))
    val_acc_metric.reset_states()

기본적으로 Custom Training Loop는 위와 같이 구현된다. 이걸 하나하나 뜯어서 설명해 보도록 하겠다.

1. tf.GradientTape()

   tensorflow 2의 핵심인 AutoGrad를 구동시켜주는 친구이다. 이 tape scope 안에서 실행된 tensorflow operation들은 back propagation을 위한 AutoGrad 미분 그래프의 구축이 시작된다.

2. tape.gradient

   이 함수를 실행하면 구축된 AutoGrad 미분 그래프를 따라서 미분이 시작된다.

3. apply_gradients

   이는 optimizer(ex. Adam)의 method이고 tape.gradient에서 구한 gradient를 사용자가 정한 optimizing algorithm을 통해서 Weight를 업데이트 해준다.

4. update_state

   이는 학습 과정중에서 측정할 수 있는 Metric들을 구하는데 사용된다. (ex. 정확도) keras에서 제공하거나 직접 만든 Metric 객체를 새로 Nerual Network에서 계산된 batch에 적용하고 싶을때 사용한다.

이렇게 Custom Training loop는 크게 4가지 요소로 구성된다.
필자는 이것을 보통 템플릿으로 가지고 개발할때마다 조금씩 바꿔서 사용하는 편이다. 독자들도 조금 복잡한 트릭이 필요한 Neural Network를 구현할때 본인만의 Training loop를 구성하고 조금씩 바꿔가면서 사용하는 것을 추천한다.

다음으로 다룰 것은 Custom loss이다.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25

# Custom Loss
class CustomMSE(keras.losses.Loss):
    def __init__(self, **kwargs):
        super().__init__(**kwargs)
    
    def call(self, y_true, y_pred):
        # tf.math.square : 성분별 제곱
        # [1,2,3] ==> [1,4,9]
        L = tf.math.square(y_true - y_pred)
        # tf.math.reduce_sum: 벡터 합.
        # [1,2,3] ==> 6
        L = tf.math.reduce_mean(L)
        return L

# Custom Regularizer(규제 ==> MAP)
class CustomRegularizer(keras.regularizers.Regularizer):
    def __init__(self, _factor):
        super().__init__()
        self.factor = _factor
    
    def call(self, weights):
        return tf.math.reduce_sum(tf.math.abs(self.factor * weights))
    
    def get_config(self):
        return {"factor" : self.factor} # 모델을 저장할때 custom layer, loss, 등등을 저장할때 같이 저장해 주는 역할.

tensorflow는 사용자가 Loss나 Regularizer까지도 자유롭게 구성할 수 있도록 허락해준다. 사용 방법은 기존 loss들과 똑같다. 그저 자신이 원하는 연산들을 생각해서 구현하면 된다.

이걸로 Optimization part.B를 마치도록 하겠다. 이 정도까지 Custom해서 사용할 사람들은 많이 없겠지만 혹시라도 필요한 사람들이 있을까 싶어서 적어 보았다.

본 포스트는 Hands-on Machine learning 2nd Edition, CS231n, Tensorflow 공식 document, Pattern Recognition and Machine Learning, Deep learning(Ian Goodfellow 저)을 참조하여 작성되었음을 알립니다.

Index

1. Essential Mathematics
   • Basic of Bayesian Statistics
   • Information Theory
   • Gradient
2. Loss Function Examples
3. What is Optimizer?
4. Optimizer examples
5. Partice

여기서는 1~4는 Part. A이고 5는 Part. B에서 다루도록 하겠다.

Essential Mathematics

Basic of Bayesian Statistics

이 파트에서는 Bayesian Statistics에 대해서 매~우 간단하게 다루어 보도록 하겠다. 실은 다룬다고 말하는 것도 부끄러울 정도록만 할 예정이니 너무 기대는 하지 않아 주었으면 한다.

여기서는 조금 익숙하지 않은 통계학, Bayesian 통계학을 소개하도록 할 것이다. 이 분야는 패턴 인식에서 아주 많이 활용되며, 기존의 확률론에 익숙해져 있다면 이를 받아들이기 매우 힘들다.

우선, “확률”이란 무엇인지에 대해 논하고 넘어가자.
Frequentist – “빈도”에 대한 척도, 어떤 일이 앞으로 얼마나 일어날 수 있겠는가?
Bayesian – 불확실성에 대한 척도, 이 가설에 대해 얼마나 확신할 수 있는가?

Bayesian 관점에서의 확률을 그림으로 표현하자면 대충 아래와 같다

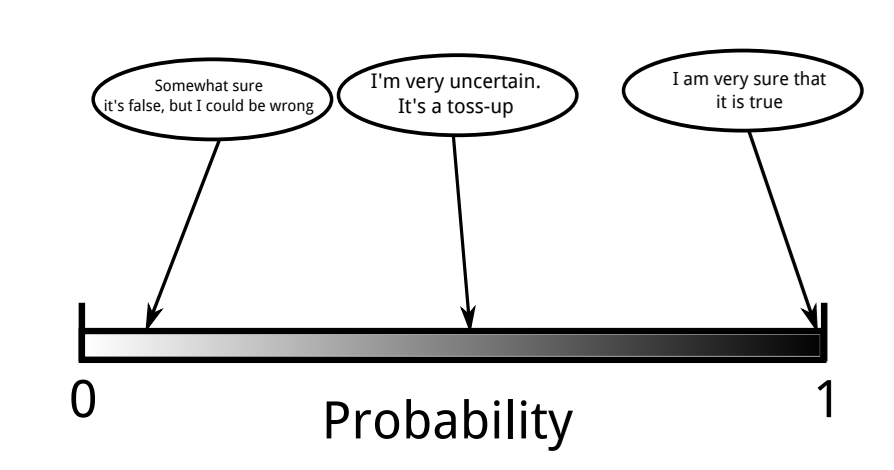
간단하게만 말하자면, 확률이 1에 가까울수록 “명제의 참에 대한 확신”을 가질 수 있고 0에 가까울 수록 그 반대인 것이다. 그리고 0.5에 가까워 질수록 점점 애매해 지는 것이다.

그리고 이 관점에서 우리는 다음 3가지 개념을 다뤄 볼 것이다.

1. Prior Probability
2. Likelihood
3. Posterior Probability

이 3가지를 말로 풀어서 설명하면 다음과 같다.

1. Prior Probability: 데이터가 주어지기 전에 우리의 가설은 얼마나 타당한가?
2. Likelihood: 어떤 데이터들이 특정 확률 분포에서 추출되었을 확률
3. Posterior Probability: 주어진 데이터에 한에서 우리의 가설이 얼마나 타당한가?

우리는 이들애 대해서 엄밀한 정의를 다루는 것이 아닌, 좀 더 실용적인 측면에서 예제와 함께 다루어 볼 것이다.

이를 활용하는 예제로써 한번 Curve fitting 문제를 생각해 보자. Curve fitting을 하기 위해서 우리는 어떤 parameter $w$를 가지고 이를 우리가 원하는 곡선에 맞게 fitting하는 과정을 거칠 것이다.

우리는 이때 이런 가정을 할 수 있다.
“parameter $𝑤$로 생성된 곡선 $𝐶$는 주어진 데이터 $𝐷$를 잘 설명할 수 있다.”
이 문장은 특정한 불확실성을 가지고 있다. 당연히 처음부터 Fitting이 잘 될 리도 없고, 특정한 에러를 가지고 있음이 분명하다.

이렇다면 우리는 그 불확실성을 어떻게 확률로 표현 가능하겠는가? 한번 다음과 같이 해보자.

$Pr(w)$: 데이터가 주어지기 이전에 위의 가설이 얼마나 확실한가
$Pr(D|w)$: 주어진 모델에서 데이터가 얼마나 잘 설명되는 가의 척도
$Pr(w|D)$: 데이터가 주어졌을 때, 이 모델이 데이터를 잘 설명하는 가의 척도

이때, 좋은 모델을 만드는 방법은 크게 2가지가 있다.

1. Likelihood를 최대화하는 parameter 만들기 ==> MLE(Maximum Likelihood Estimation)
2. Posterior Probability를 최대화하는 parameter 만들기 ==> MAP (Maximum A Posterior)

즉, 1번 방법은 최대한 좋은 주어진 모델에서 최대한 좋은 데이터의 설명을 얻어내는 방법이고, 2번 방법은 데이터를 가지고 최대한 좋은 모델을 얻어내는 방법이다.

이 관점에서 1번부터 차근차근 설명해 보도록 하겠다. 어떻게 하면 likelihood를 최대화할 수 있을까?

우선 $Pr(D|w)$의 함수를 찾아서 이를 최대로 만들어 주면 되는 것이다. 최대로 만들어 주는 방법은 여러가지 방법이 있겠지만, 우선 그것보다 $Pr(D|w)$를 찾는 것부터 진행하는 것이 순서일 것이다.

그 전에 표현을 좀 정리하고 가겠다.

자, 그리고 우리는 다음과 같이 “가정”을 해보자.
데이터에서 주어진 target값과 우리의 예측 값의 차이가 Gaussian Distribution을 따른다

이를 수식으로 표현하면 다음과 같다.

여기서 $\epsilon_i$는 실측값과 데이터 간의 오차이다. ($\epsilon_i = t_i - y(x_i;w)$)

즉, 우리가 고등학교에서 확률과 통계를 착실히 배웠다면 다음과 같이 변형이 가능할 것이다.

위의 내용을 시각화 하면 대충 다음과 같다.

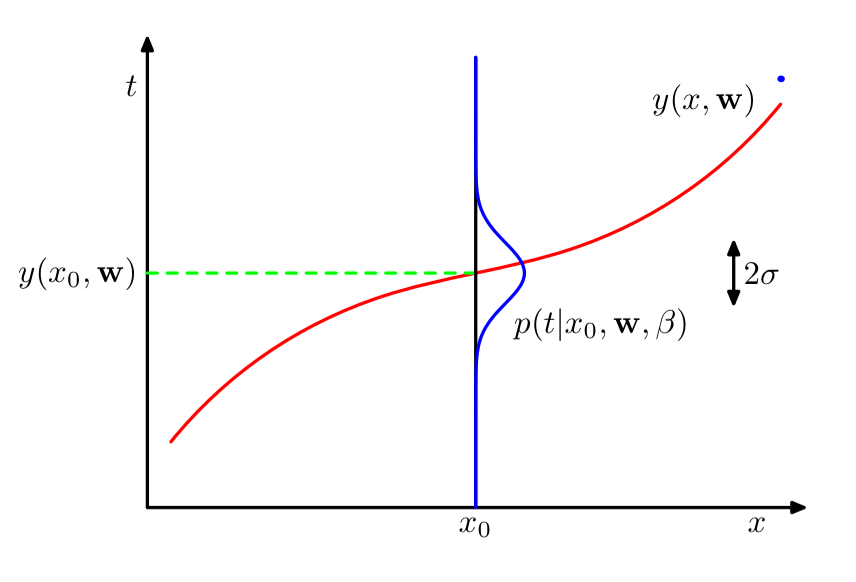
이제 각각의 데이터에 대해서 이를 정의해 놓았으니, 데이터 전체에 대해서는 각각의 데이터가 i.i.d라는 가정 하게 그냥 곱해주면 된다. 다음과 같이 말이다.

자, 이제야 뭔가 손에 잡히는 느낌이 든다(아닌가?!?)
자세히 보면 위 식이 likelihood 아닌가? 정의 그대로이다.

이제 위의 Probability를 최대화 하면 되는 것이다.
근데 product는 다루기 어려우니 만능 툴인 로그를 씌워 보자.

이때, 우리는 2가지 parameter에 대해서 위 식의 최대값을 구해야 한다. 첫번째가 $w$이고 두번째가 $\beta$이다.
우선 $\beta$부터 해보자면 다음과 같이 가능하다.

결국 이 미분 값을 0으로 만드는 값이 최대값일 것이므로 다음과 같이 식을 풀어낼 수 있다.

이제 $w$에 대해서 최대값을 구해보면 다음과 같다.

어..? 어디서 많이 본 것 같지만 일단 넘어가자. (실은 나중에 loss function 부분에서 한번 더 다루겠다.)

여기서의 최적화는 다양한 방법으로 시도할 수 있다.

이의 원리를 다시 한번 떠올려보자.

1. 에러가 Gaussian Distribution을 따를 때,
2. 주어진 데이터 𝐷를 우리의 model이 데이터를 잘 설명할 수 있다는 가설이
3. 참일 것이라는 확률(확실성)을 높이는 과정

이것이 바로 우리가 진행한 것이다.

그렇다면, 이제 MAP를 활용해서 이를 구해보면 어떻게 될까?
Bayes’ Theorem에 따라 구하면 다음과 같이 작성 가능하다.

위 식에서 뭔가 낯설지만 익숙한 것이 보인다. 바로 $Pr(w|\alpha)$이다. 이것이 바로 “사전 확률”이다.

사전 확률 또한 우리가 모르지만, 일단 만능인 Gaussian 이라고 가정해 보자. (이 가정이 나름의 타당성을 갖춘다는 것을 알고 싶으면 확률 및 랜덤 변수를 조금 깊게 공부해 보자.)

그렇다면, 우리는 이를 통해서 최대 (로그)사후 확률을 마찬가지로 미분을 통해서 구해보면 다음과 같다.

이것도 뭔가 어디서 본 것 같은데..? 라고 생각한다면 당신은 멋진 사람 :)

이걸로 Bayesian Statistics에서 말하는 likelihood와 prior/posterior 확률이 어떤 개념인지 조금이라도 와 닿았으면 좋겠다 ㅎㅎ.

Information Theory

이 파트에서는 정보 이론을 매~~~~우 간단하게만 다루어볼 예정이다. 이것도 다룬다고 말하기도 부끄럽다고 할 수 있을 정도로만 다루도록 하겠다.

정보 이론은 “정보량”의 개념으로부터 시작한다. 이것이 현대에 들어서 통신, 패턴 인식 등 여러 분야에 사용되고 있다.
그리고 이러한 정보량의 평균을 “엔트로피”라고 부른다.

정보량은 다음과 같이 정의된다.

한가지 예를 들어 보겠다. 다음과 같이 정의되는 랜덤 변수가 있다고 가정해 보자.

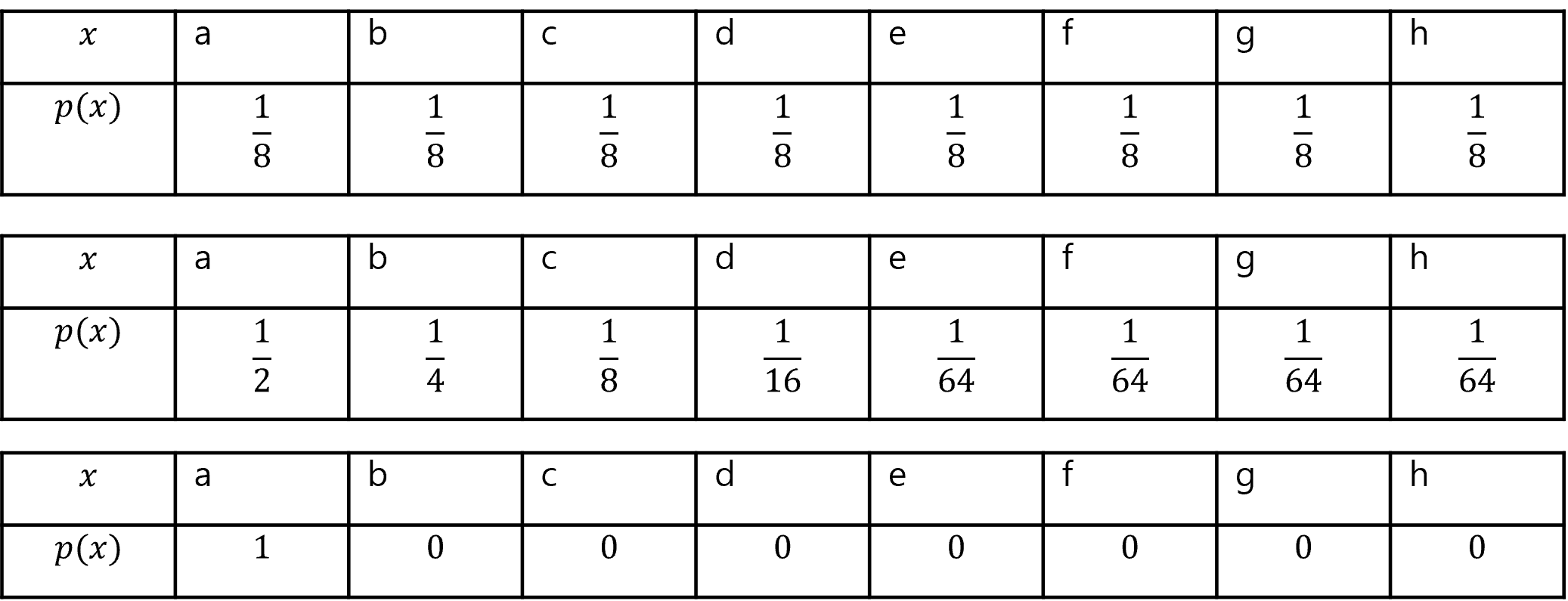
이의 엔트로피를 구해보면 다음과 같다.

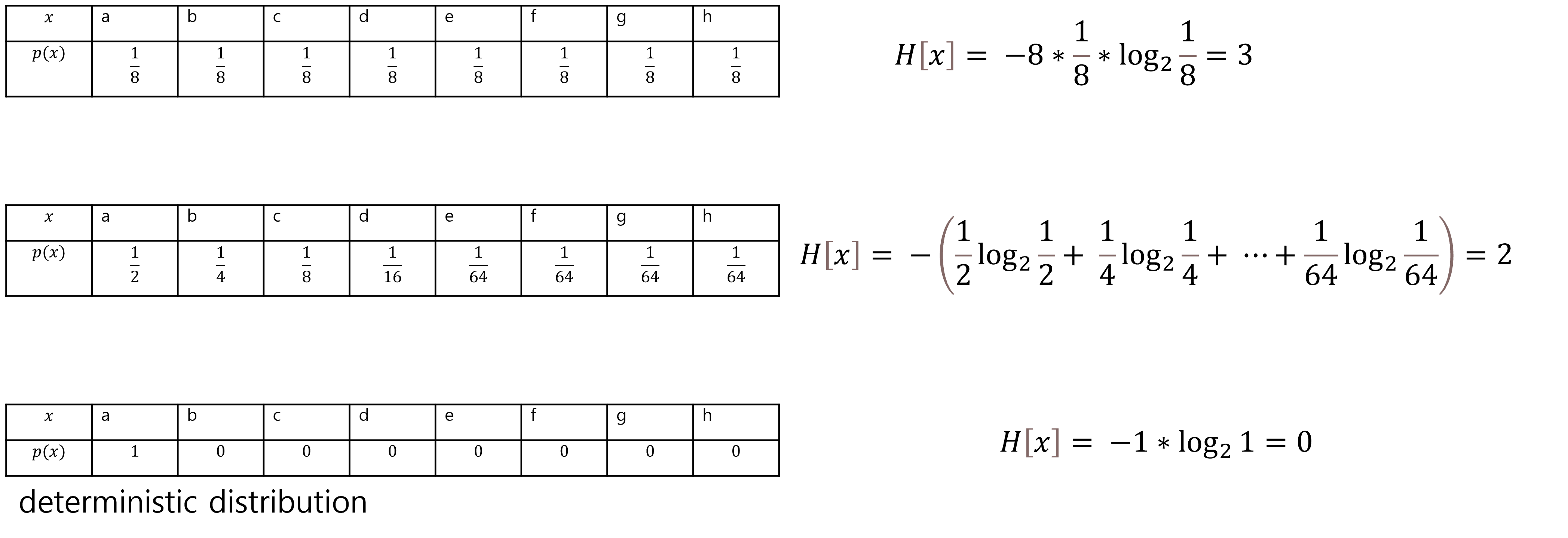
이 내용을 갑자기 왜 하느냐? 우리는 다른 2개의 확률분포의 상대적 엔트로피와 상호 정보량을 계산하여 2개의 확률분포의 차이를 정량화 할 수 있기 때문이다.

우선, 우리가 근사를 목표로 하는 확률 분포를 $𝑝(𝑥)$라고 해보자.
이를 근사하기 위해서 모델을 학습시켜서 확률 분포 $𝑞(𝑥)$를 얻어 냈다고 치자.
이때, $𝑞(𝑥)$를 통해서 얻어낸 정보는 원래 $𝑝(𝑥)$를 통해서 얻을 수 있는 정보와 상이할 것이고, 우리는 이에 추가로 필요한 정보량의 평균을 다음과 같이 구할 수 있을 것이다.

자, 그렇다면 우리는 대충 궤가 보인다. 우리가 결국 학습시켜야 하는 분포 $𝑞(𝑥)$와 정답인 분포 $𝑝(𝑥)$사이의 차이를 정량화 해주는 함수가 바로 이것인 것이다.
이를 “쿨백-라이브러리 발산”이라고 하며, 이를 통해서 우리는 두 확률 분포의 차이를 알 수 있는데,
자세히 보니, 뒤의 목표 분포의 엔트로피는 그냥 상수나 다름이 없다. 따라서 앞의 항만을 따서 따로 “Cross-Entropy”라고 하며, 다음과 같이 표현할 수 있다.

Gradient

이 파트에서는 대학교에서 Calculus를 배우지 않은 (배웠다 하더라도 다변수 함수의 미분 파트를 안 들은 이들) 사람들이 꼭 보아 주었으면 한다. Gradient의 기초 중의 기초를 다룰 예정이다.

우리는 이전 시간에 결국에는 미분을 구해서 가중치를 update하는 것이라고 배워왔다.
근데, 이때 “Gradient”라는 것에 대한 명확한 설명 없이, 그냥 하면 된다는 식으로 짚고 넘어갔던 기억이 난다.

우선, 함수에서 몇가지 예시부터 생각하고 넘어가자.

1. $f: \mathbb{R}^1 \rightarrow \mathbb{R}^1$
2. $f: \mathbb{R}^N \rightarrow \mathbb{R}^1$
3. $f: \mathbb{R}^1 \rightarrow \mathbb{R}^N$
4. $f: \mathbb{R}^N \rightarrow \mathbb{R}^M$

이때, $N,M \geq 2$이다.

$\mathbb{R}^1$을 따로 분리한 이유가 있다. 함수에서 입/출력이 벡터(또는 행렬)인 것과 입/출력이 Scalar인 것은 다소 상이한 과정을 도입해야 하기 때문이다. 우리는 이 중에서도 2번을 특히 중요하게 다룰 것이다.

이렇게 함수는 여러가지 형태가 있을 수 있는데 이때, 각각 정의역에 대한 미분이 어떻게 정의될까?
이 파트에서는 그 예시를 들어볼 것이다.

우선, $f: \mathbb{R}^N \rightarrow \mathbb{R}^1$ 에서의 경우를 보자. 일 변수 스칼라 함수의 경우는 빼겠다. 그걸 모르면 이걸 들을 자격이 없다.

우리는 이러한 함수를 vector-scalar함수라고 부르겠다.
이러한 함수의 미분은 다음과 같이 정의할 수 있다.

이렇게 정의되어 있을 때, 함수 $f$에 대한 Gradient는 다음과 같이 표현되고 정의된다.

여기서 만약 입력이 행렬이면 어떻게 되어야 할까?
즉, 다음과 같이 출력이 Scalar이고 입력이 벡터인 함수이다. (Matrix-Scalar함수)

Loss Function Examples

이 파트에서는 위에서 배운 수학적인 기초를 토대로 Loss function의 예시를 한번 볼 것이다.

우선 MSE부터 생각해 보자. 결국 MSE는 MLE/MAP를 이론적인 기저로 두고 있었다는 것을 위 글을 읽었다면 이해할 수 있었을 것이다. $equation 5$를 다시 한번 봐보자.

그렇다면 Cross-Entropy를 어떻게 사용할 것인가?
신경망에서는 이를 분류 문제를 어떻게 풀까? 우리는 Softmax 함수를 같이 사용하여 이를 해결할 수 있다.

먼저 softmax 함수부터 생각해 보자.

위 함수를 Neural Network에서 output layer의 각 출력 값을 확률 분포로 바꾸어 준다고 생각하면 된다. 실제로 모든 unit의 값을 다 더하면 1이 되니깐 말이다.

이제 이러한 확률 분포를 토대로 실제 우리가 원하는 target 확률 분포와의 거리를 구하는 과정을 Cross entropy로 진행할 수 있을 것이다. 다음과 같이 말이다.

이때, target 분포는 class에 따라 one-hot encoding이 되어 있음
이때, 이 함수를 미분하면 어떻게 될까? 다음을 한번 보자.

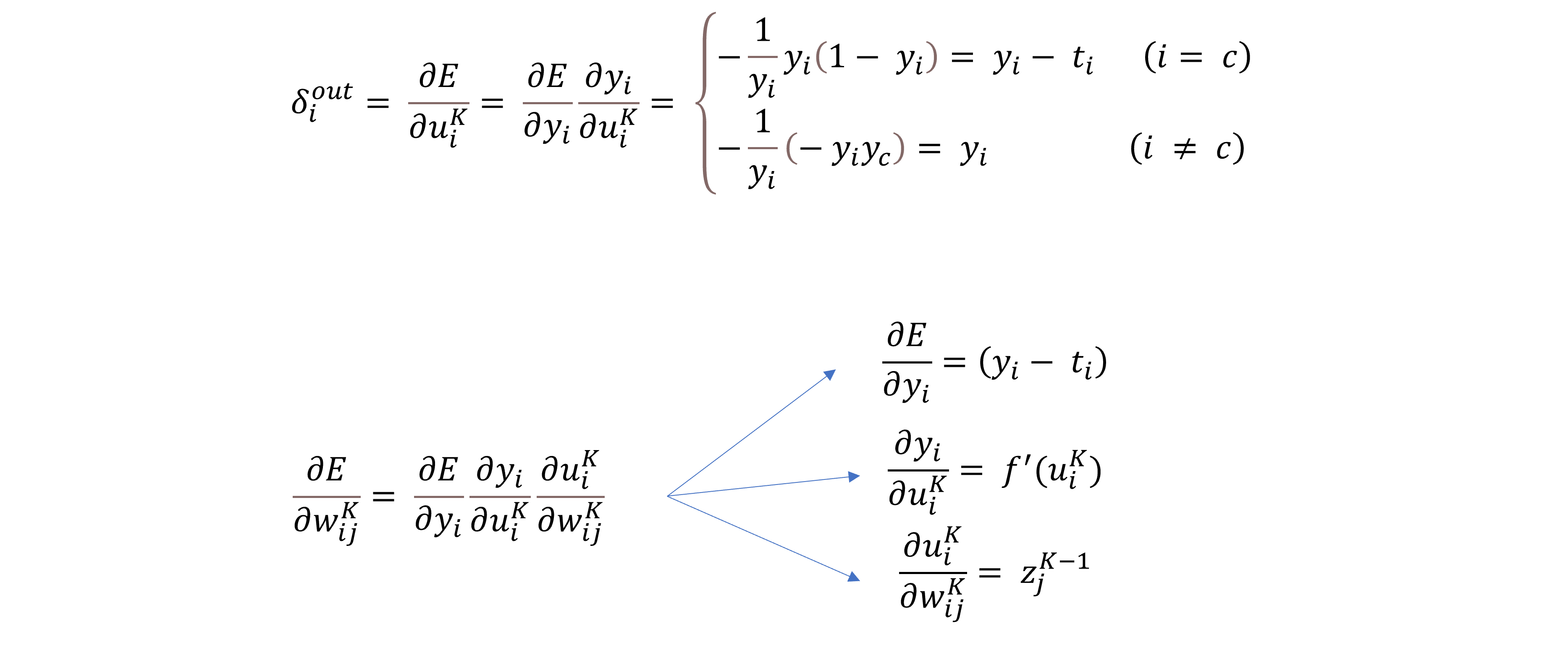
결국 형태가 One hot encoding이 되어 있다면, MSE와 딱히 다를 것이 없다는 것을 알 수 있다.

What is Optimizer?

이 파트에서는 위에서 배운 수학적 기초를 토대로 Optimizer가 어떻게 동작을 하는 놈들인지 배워 보도록 하겠다.

그래서 Deep learning에서의 Optimizer는 어떤 역할인지 알아보자. 결국 Deep learning은 해당 문제를 해결하는 것에 중심을 두고 있다. 이때, 우리는 특정한 문제를 해결한다고 했을 때, 특정 지표(ex. 정확도)를 최대화 한다는 것이다.
우리는 이때 정확도를 최대화 하기 위해서 데이터에서 얻을 수 있는 손실(Loss)를 최소화하는 것을 진행한다. 이는 기존 최적화와는 조금 다르다. 직접 지표를 최대화하는 것이 아닌, 간접적인 지표를 최소화하는 방향으로 가는 것이니 말이다.

그래서, 결국 Optimizer의 역할이 무엇인가?
다음과 같다.

이게 뭐냐? 즉 데이터에 대한 손실을 최소화 하는 것이다. 이것이 Optimizer 의 궁극적인 역할인 것이다.
이 문제는 1줄만 생각해 보면 간단해 보이지만 실은 겁나게 어렵고 복잡한 문제이다.
이 문제를 풀기 위해서 우리는 Gradient Descent라는 방법을 사용하는 것이다.

여기서 Gradient Descent의 수렴성을 설명하고 싶지만…. 강의에서는 생략하도록 하겠다. 더 자세히 알고 싶으면 Talyor 급수를 키워드로 잘 찾아보기를 바란다. 만약 나중에 시간이 된다면 다시 다루어 보도록 하겠다.

이쯤에서 미니 배치의 의미를 설명하고 가도록 하겠다.
이 것은 다음 그림으로 설명이 될 수 있다.

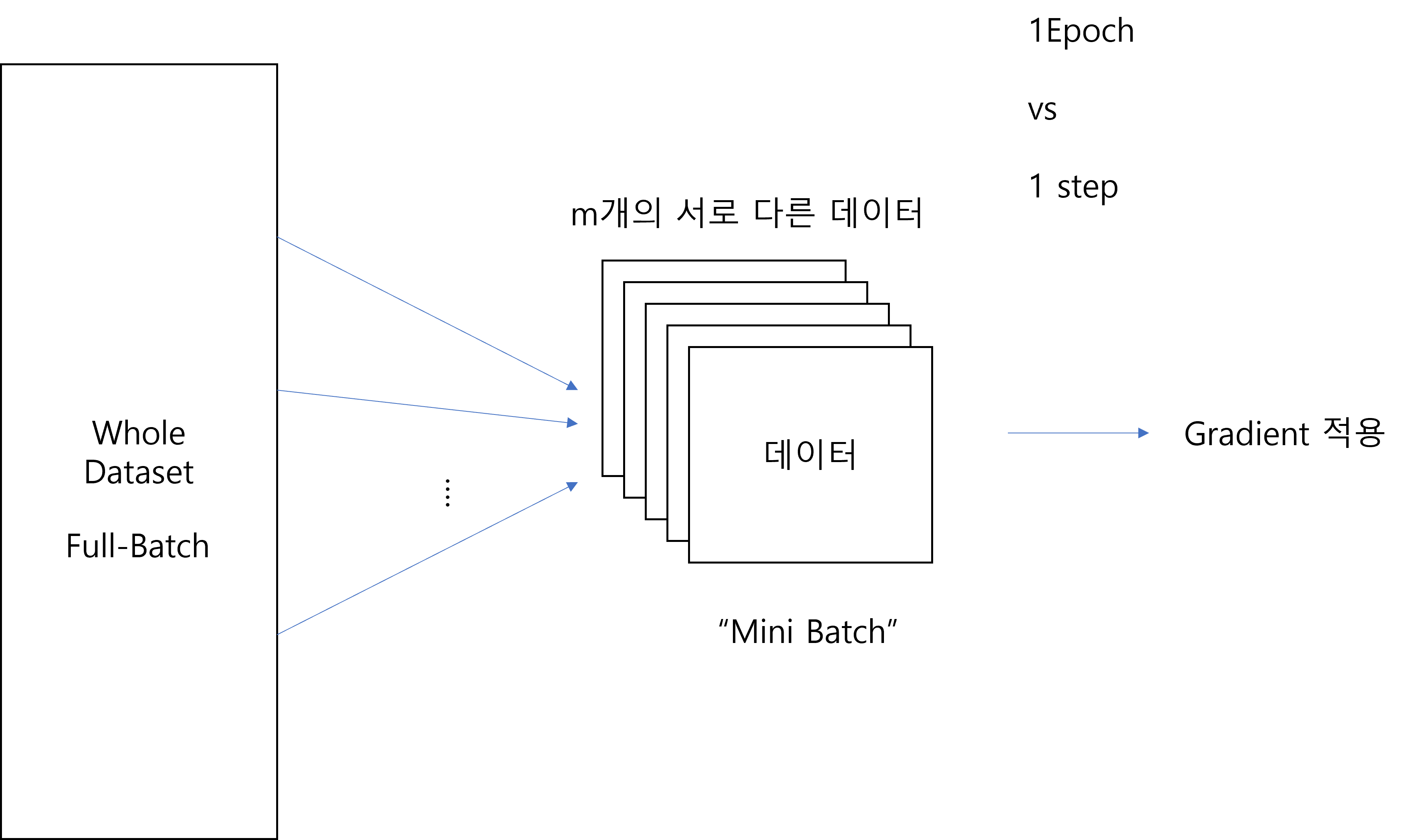
~역시 필자는 필자 스스로 생각해도 발 그림이다. 당도췌 어떤 정신머리로 이딴걸 그리는지 모르겠다.~

자 각설하고, 전체 데이터에서 정해진 Batch Size 만큼을 뽑아서 만든 데이터를 Mini Batch라고 한다. 이를 신경망에 넣어서 Feed Forward를 하고 Back propagation 연산을 하면서 가중치를 업데이트한다. 이것이 학습의 1개의 step이다. 그리고 이 mini batch set으로 전부의 데이터를 학습 했을때, 그것을 1개의 epoch이라고 한다. (통상적으로) 이렇게만 간단하게 생각하고 나머지는 Optimizer 별로 따로 생각하면 편할 것이다.

Optimizer examples

이 파트에서는 Optimizer의 종류가 어떤 것들이 있는지 알아보도록 하겠다.

1. Stochastic Gradient Descent

이 Optimizer는 가장 간단한 Optimizer라고 생각해도 된다. 위에서 설명한 대로, 간단하게 Mini Batch를 뽑아서 Update를 진행한다.

1. Adagrad

이 방법은 이전에 사용했던 gradient들을 축적해서 사용하는 방법이다. gradient를 원소별로 제곱해서 step별로 더해가는 행렬을 하나 만들고, 그 행렬을 update할때 gradient에 원소별로 곱해주는 것이다. 제목 그대로 Adaptive gradient 방법인 것이다.

1. RMSProp

이 방법은 위의 Adagrad 방법에서 조금 더 나아가, gradient를 더해나갈때 가중치를 두는 방법이다.

1. Adam

현재 가장 많이들 쓰는 Optimizer이다. 이것도 별거 없다. RMSProp 처럼 가중합을 진행하는데, 이번에는 원소별로 제곱하지 않은 gradient도 누적 합을 저장해서 사용한다. 자세한 것을 수식을 보면 바로 감이 올 것이다.

이걸로 Optimization 파트 A는 끝이 났다. 다음 파트는 위에서 배운 것들을 구현하면서 찾아 오도록 할 것이다.

본 포스트는 Hands-on Machine learning 2nd Edition, CS231n, Tensorflow 공식 document를 참조하여 작성되었음을 알립니다.

Index

1. Definition of Recurrent Neural Network(RNN)
2. Back Propagation of RNN
3. Partice

여기서는 1,2는 Part. A이고 3은 Part. B에서 다루도록 하겠다.

Definition of Recurrent Neural Network(RNN)

RNN(Recurrent Neural Network)은 시계열 데이터를 처리하는데 특화된 신경망 구조이다.
이는 전의 입력이 연속해서 다음 입력에 영향을 주는 신경망 구조로써, 같은 구조가 계속 순환되어 나타나기 때문에 이러한 이름이 붙어져 있다.
다음 그림을 보자.

하지만 이 그림으로는 자세한 구조까지는 잘 모르겠다. 그래서 필자가 직접 그린 그림을 보면서 설명하도록 하겠다. 말해두겠지만 필자는 그림을 심각하게 못 그리니 양해 바란다.

이처럼 각 RNN Cell에 FCNN의 Unit이 들어가 있는 형식으로 구현된다. 이의 Feed Forward 연산을 생각해 보면 정말 간단하다.

$equation\space 1$에서 각 변수들의 정의는 다음과 같다.

Definition 1

• $z_t$: time step $t$에 unit의 값에 activation function에 넣은 값
• $W_{re}$: Reccurent 가중치
• $W_{in}$: input layer에서의 가중치
• $x_t$: input vector

그림으로 정리하면 대충 다음과 같다.

결국 이렇게 Sequential한 데이터 $x$에 대해서 Sequential한 output $y$를 뽑을 수 있는 것이다.

Back Propagation of RNN

RNN의 Back Propagation 방법은 다음의 2가지가 있다.

• Back Propagation Through Time - (BPTT)
• Real Time Recurrent Learning (RTRL)

여기서는 BPTT만을 다루도록 하겠다. RNN을 그렇게 자세하게 다루지 않는 이유는 FCNN의 연장선 느낌이 강해서이고 또한 현대에서는 딱히 잘 쓰이지 않기 때문이다. 그냥 지적 유희를 위해서 또는 기본기를 잘 닦기 위해서로만 읽어주기를 바란다.

또는 AutoGrad 계열의 알고리즘을 공부하는 사람들은 미분 그래프를 사용한 AutoGrad이전에는 이런 식으로 역전파 알고리즘을 구현했었구나 라고 역사책 읽는 느낌으로 읽어주면 매우 감사하겠다.

이러한 RNN의 Back Propagation을 진행하기 위해서는 다음을 구하면 된다.

이제 위 미분들에 chain rule을 적용해 보자. 그렇다면 다음과 같이 표현할 수 있다.

자, 그렇다면 여기서 delta를 정의해서 일반화된 delta 규칙을 적용해 보아야 Back Propagation이 효율적으로 될 것이다.

그렇다면 각 미분들에 대한 delta는 다음과 같이 정의될 수 있다.

input layer에서의 가중치는 output layer처럼 FCNN과 완전히 같다. 굳이 적어두지는 않도록 하겠다. 그렇다면 남은 것은 recurrent layer에서의 delta이다. 전개해보면 대략 다음과 같이 표현할 수 있다.

이를 수식으로 표현하면 다음과 같이 표현할 수 있다.

각 Summation Term들의 delta를 이용해서 표현해 보면 다음과 같다.

즉, 이와 같이 RNN Cell의 기본 형태의 BPTT는 정말 단순하게도 FCNN의 연장선이다. 별게 없다.

그리고 이의 변형판으로 시간을 분할해서 Update하는 방법도 있다. 이를 Truncated BPTT라고 하는데 관심이 있다면 찾아보도록 하자. 이것도 진짜 별거 없다.

그저 위의 미분에서 시간 term을 잘라서 update 해주면 된다.

이걸로 RNN 또한 끝이 났다. 다음 파트에서는 이를 구현해 보도록 하겠다.

본 포스트는 Hands-on Machine learning 2nd Edition, CS231n, Tensorflow 공식 document를 참조하여 작성되었음을 알립니다.

Index

1. Definition of Recurrent Neural Network(RNN)
2. Back Propagation of RNN
3. Partice

Partice

진짜 여기까지 과연 읽은 사람이 있을까 싶다. 있다면 압도적 감사의 의미로 그랜절을 박고 싶은 마음이다. ㅋㅋ

장난은 그만하고 오늘도 시작하자. 오늘도 역시 Model Subclassing API를 활용하여 간단하게 RNN을 활용하는 예제를 구현해볼 것이다.

우선 RNN을 tensorflow에서 어떻게 사용할 수 있는지부터 보자.

1
2
3
4
5
6
7
8
9
10
11

class RNNLayer(keras.Model):
    def __init__(self, num_hidden=128, num_class=39):
        super(RNNLayer, self).__init__()
        self.RNN1 = keras.layers.SimpleRNN(num_hidden, activation='tanh', return_sequences=True)
        self.out = keras.layers.Dense(num_class, activation="softmax")
        self.out = keras.layers.TimeDistributed(self.out)
        
    def call(self, x):
        x = self.RNN1(x)
        out = self.out(x)
        return out

보면 알다시피 아주 간단하다. 그래서 이번 포스트에서는 간단하게 2개의 관전 포인트만을 다루려고 한다.

1. SimpleRNN layer의 특징
2. TimeDistributed layer의 특징

1번부터 차례로 시작하자.

우선 SimpleRNN을 이해하려면 입력으로는 어떤 tensor를 받아먹어서 출력으로는 어떤 tensor를 뱉어내는지를 알아야 한다.
지난 포스트에서 RNN의 구조를 보았다면 당연히 입력은 시간순서대로 벡터가 들어가니 적어도 3차원(배치까지 포함해서) 일 것이고 출력도 시간 순서대로 나와야 하니 같은 3차원이라는 것 쯤은 유추가 가능할 것이다. 하지만 실제로는 이것 또한 조절이 가능하다.

1
2
3
4
5
6
7
8
9
10

keras.layers.SimpleRNN(
    units, activation='tanh', use_bias=True,
    kernel_initializer='glorot_uniform',
    recurrent_initializer='orthogonal',
    bias_initializer='zeros', kernel_regularizer=None,
    recurrent_regularizer=None, bias_regularizer=None, activity_regularizer=None,
    kernel_constraint=None, recurrent_constraint=None, bias_constraint=None,
    dropout=0.0, recurrent_dropout=0.0, return_sequences=False, return_state=False,
    go_backwards=False, stateful=False, unroll=False, **kwargs
)

이는 tensorflow 공식 문서에 적혀 있는 SimpleRNN에 관한 내용이다. 여기서 우리가 관심 있게 봐야 할 것은 return_sequences와 return_state이다.

만약, return_sequences가 False면, SimpleRNN layer는 맨 마지막의 출력만을 뱉어낸다. 즉, 2차원 출력이 되는 것이다. ([Batch_size, output_dim]) 하지만 이 파라미터가 True이면 모든 시간의 출력을 출력으로 내뱉는다. 즉, 3차원 출력이 되는 것이다.

그리고 return_state의 경우, 이것이 True이면 출력의 Hidden State를 출력으로 같이 내뱉는다. 즉, 출력이 tuple이 되는 것이다. (출력 벡터, hidden 벡터)

이렇게 되면 우리는 여러가지 경우의 수를 고려해서 모델을 만드는 것이 가능해진다.

1. 맨 마지막 출력만을 고려하여 예측하는 모델
2. 입력마다 다음에 나올 출력을 예측하는 모델

전자를 Many to One, 후자를 Many to Many라고 한다.

그렇다면 Many to Many를 해주기 위해서는 시간 순서에 맞춰서 같은 Dense layer를 적용해줄 필요가 있다. 이를 위해서 필요한 것이 바로 TimeDistributed layer이다. 이는 각 시간 step에 대해서 같은 Dense layer의 weight로 연산을 진행해 준다.

하지만 기본적으로 tensorflow에서 Dense layer는 broadcast 기능을 제공한다. 따라서 굳이 TimeDistributed layer 없이도 3차원 텐서가 들어오면 맨 마지막 차원에 대해서 Dense 연산을 진행하게 된다.

따라서, Dense만을 사용할거면 굳이 TimeDistributed layer가 필요 없다.

RNN의 포스팅은 이걸로 마치도록 하겠다. 딱히 크게 어려운 점도 없고 나중에 나올 Attention이 훨씬 더 어그로가 끌려야할 주제이기 때문이다.

본 포스트는 Hands-on Machine learning 2nd Edition, CS231n, Tensorflow 공식 document를 참조하여 작성되었음을 알립니다.

Index

1. Introduction of Convolution Operation
2. Definition of Convolutional Neural Network(CNN)
3. Back Propagation of CNN
4. Partice

6. Partice

이 파트는 Convolutional Nerual Network를 직접 구현하는 파트이다. 비단 Convolutional Neural Network 뿐만 아니라 그를 이용한 다양한 현대적인 네트워크 구조들을 구현해 보는 시간을 가지도록 하겠다. 필자의 Deep learning 구현 관련 블로그 포스팅은 전부 Model Subclassing API로 구현될 예정이다. 왜냐? 필자 맘이다 (꼬우면 보지 말든가) 장닌이고, 필자가 생각하기에는 Model Subclassing API의 활용 장점은 확실히 있는 것 같다.

1. 모델을 가독성 있게 관리할 수 있다.

   이는 전적으로 OOP에 대한 기본 개념 및 디자인 패턴을 잘 아는 사람에 한에서 그런거다.
   Vision Transformer쯤 가면 알겠지만, 정말 짜야하는 연산들이 엄청 많다. 그런걸 하나하나 함수로 짜거나 Sequential API로 구성하면 지옥문이 열리게 된다. 아 물론 짜는건 무리가 없겠지만, 유지보수 관점에서는 정말 지옥일 것이다.
   그런 의미에서 Model Subclassing API는 원하는 연산을 Class단위로 묶어서 설계하고 그들을 체계적으로 관리할 수 있는 지식이 조금이라도 있다면 (복잡한 디자인 패턴까지는 필요도 없다) 훨씬 가독성이 높은 코드를 짤 수 있다.

2. Low Level한 연산을 자유롭게 정의할 수 있다.

   Model Subclassing API를 사용하면 Custom Layer, Scheduler 등등 여러 연산을 사용자의 입맛에 맞게 정의할 수 있다. 이러면 내가 세운 새로운 가설, 연구 아이디어를 보다 쉽게 구현할 수 있는 판로가 열리는 것이다. 물론 이는 전적으로 자신이 새로운 연산을 구상하고 구현할만한 경지에 도달했을때의 이야기이다.

3. 특히 Pytorch로 소스코드 전환을 비교적 쉽게 할 수 있다.

   이건 지극히 필자의 개인적인 생각이다. 필자는 pytorch와 tensorflow를 동시에 써가면서 일을 하고 있다. 모델 개발 및 연구는 pytorch로 배포는 tensorflow를 사용하고 있는데, 모델을 tensorflow로 완전히 포팅해야할 일이 가끔씩 있다. 이때 model subclassing API를 활용하는 편이 소스코드의 구조나 뽄새가 비슷해서 편했던 기억이 난다.

하지만 단점도 명확하게 있다.

1. 못쓰면 이도 저도 안된다.

   보면 알다시피, OOP의 기초 지식과 low level로 연산을 정의해서 사용할 수 있는 사람이 아니라면 굳이 Subclassing API를 쓰겠다고 깝치다가 되려 오류만 범할 가능성이 높다.

하지만 필자는 앞으로 잘하고 싶어서 힘든 길을 골라 보았다. 독자들도 이에 동의하리라고 믿는다. (아니면 뒤로 가든가)

사족이 길었는데, 앞으로도 계속 Model Subclassing API만을 사용해서 포스팅을 할 예정이다.

우선, 지난 FCNN처럼 tensorflow 2로 어떻게 CNN layer를 정의할 수 있는지부터 알아보자.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48

class CustomConv2D(keras.layers.Layer):
    #              1. output image의 채널  2. 커널의 이미지 사이즈  3. Stride를 정해줬어야함. 4. Pooling을 정해줬어야함.(Optional) 5. Padding을 정해야함.
    #                                                       i  x 방향으로의 stride y 방향으로의 stride      i
    # "SAME" OH = H, "VALID" 가능한 패딩 필터 중에서 가장 작은 패딩(양수)으로 설정  
    # OH = (H + 2*P - KH)/S + 1 = 15.5
    def __init__(self, out_channel, kernel_size, Strides = (1, 1, 1, 1), Padding = "SAME", trainable=True, name=None, dtype=None, dynamic=False, **kwargs):
        super().__init__(trainable=trainable, name=name, dtype=dtype, dynamic=dynamic, **kwargs)
        # "3,4" 
        self.out_channel = out_channel

        if type(kernel_size) == type(1):
            self.kernel_size = (kernel_size, kernel_size)
        elif type(kernel_size) == type(tuple()):
            self.kernel_size = kernel_size
        else:
            raise ValueError("Not a Valid Kernel Type")

        if type(Strides) == type(1):
            self.Stride = (1, Strides, Strides, 1)
        elif type(Strides) == type(tuple()):
            self.Stride = Strides
        else:
            raise ValueError("Not a Valid Stride Type")
        
        if type(Padding) == type(str()):
            self.Padding = Padding
        else :
            raise ValueError("Not a Valid Padding Type")

    def build(self, input_shape):
        WeightShape = (self.kernel_size[0], self.kernel_size[1], input_shape[-1], self.out_channel)
        self.Kernel = self.add_weight(
            shape=WeightShape,
            initializer="random_normal",
            trainable= True
        )

        self.Bias = self.add_weight(
            shape=(self.out_channel, ),
            initializer="random_normal",
            trainable=True
        )
        

    def call(self, Input):
        Out = tf.nn.conv2d(Input, self.Kernel, strides=self.Stride, padding=self.Padding)
        Out = tf.nn.bias_add(Out, self.Bias, data_format="NHWC")
        return Out

이전에도 설명했듯이 build에서 필요한 Weight를 정의한 뒤에 call에서 그것을 사용한다. 다행이게도 tensorflow에서는 최소한 convolution 연산을 정의해 주었다.
앞으로도 필요한 연산이 있다면 이렇게 정의해 주면 된다.

하지만 우리는 굳이 이렇게 convolution layer를 정의해줄 필요가 없다. 왜냐면 tensorflow keras에서 이미 정의되어 있는 좋은 함수가 있기 때문이다. 이에 대한 아주 간단한 사용 예제로써 Alexnet과 ResNet을 구현해 보도록 하겠다. 부록으로 GoogLeNet을 구현한 예제도 있는데, 이는 필자의 Github에 올려 두도록 할테니 시간이 되면 가서 봐 주었으면 한다.

우선 AlexNet부터 가보자. 모델의 구조를 사진으로 한번 봐보도록 하자.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48

class AlexNet(keras.Model):
    def __init__(self):
        super().__init__()
        # 원래 여기에는 커널 사이즈로 (11, 11)이 들어가고 padding은 valid이다. 하지만 메모리 때문에 돌아가지 않는 관계로 이미지 크기를 줄아느라 부득이하게 모델을 조금 변경했다.
        self.Conv1 = keras.layers.Conv2D(96, (3, 3), strides=(4, 4), padding="SAME", activation="relu")
        # LRN 1
        self.BatchNorm1 = keras.layers.BatchNormalization()
        self.MaxPool1 = keras.layers.MaxPool2D(pool_size=(2, 2), strides=(1, 1), padding="VALID")

        self.Conv2 = keras.layers.Conv2D(256, kernel_size=(5, 5), padding="SAME", activation="relu")
        # LRN2
        self.BatchNorm2 = keras.layers.BatchNormalization()
        self.MaxPool2 = keras.layers.MaxPool2D(pool_size=(2, 2), strides=(1, 1), padding="VALID")

        self.Conv3 = keras.layers.Conv2D(384, kernel_size=(3, 3), padding="SAME", activation="relu")
        self.Conv4 = keras.layers.Conv2D(384, kernel_size=(3, 3), padding="SAME", activation="relu")
        self.Conv5 = keras.layers.Conv2D(256, kernel_size=(3, 3), padding="SAME", activation="relu")
        self.MaxPool3 = keras.layers.MaxPool2D(pool_size=(3, 3), strides=(2, 2))

        self.Flat = keras.layers.Flatten()

        self.Dense1 = keras.layers.Dense(4096, activation="relu")
        self.DropOut1 = keras.layers.Dropout(0.5)

        self.Dense2 = keras.layers.Dense(4096, activation="relu")
        self.DropOut2 = keras.layers.Dropout(0.5)

        self.OutDense = keras.layers.Dense(10, activation="softmax")


    def call(self, Input):
        X = self.Conv1(Input)
        X = self.BatchNorm1(X)
        X = self.MaxPool2(X)
        X = self.Conv2(X)
        X = self.BatchNorm2(X)
        X = self.MaxPool2(X)
        X = self.Conv3(X)
        X = self.Conv4(X)
        X = self.Conv5(X)
        X = self.MaxPool3(X)
        X = self.Flat(X)
        X = self.Dense1(X)
        X = self.DropOut1(X)
        X = self.Dense2(X)
        X = self.DropOut2(X)
        X = self.OutDense(X)
        return X

자, 필자는 굳이 더럽게 짜 보았다. 왜냐? 이렇게 짤거면 Model Subclassing을 쓰지 말라는 의미로 이렇게 짜 보았다. 진짜 이따구로 짤거면 그냥 Sequential API나 Functional API를 사용하자. 근데 이 정도면 설명이 필요 없을 정도로 그냥 무지성 구현을 시전한 것이다. 그러니 간단하게 Keras의 Conv2D를 설명하고 넘어 가도록 하겠다.

1

keras.layers.Conv2D(filters, kernel_size=(kernel_sz, kernel_sz), padding="SAME", activation="relu")

이전에 이론 글에서 설명했던 부분을 다시 되짚어 보고 위 함수를 다시 살펴보자.

Definition 1

• $w_{ijmk}^l$: $l$번째 층의 Weight의 $k$번째 Kernel Set에 $m$번째 Channel, $i$행, $j$열의 성분

위의 $w_{ijmk}^l$를 우리는 위의 Conv2D 함수로 정의한 것이다. filters는 kernel set의 개수를 의미하며, kernel_size는 Weight kernel의 이미지 크기를 의미한다. padding은 “SAME”과 “VALID”가 있는데, “SAME”으로 하면 알아서 크기를 계산해서 입력 이미지와 출력 이미지의 크기를 같게 만든다. Valid를 선택하면 그냥 padding이 없다고 판단하면 된다.

AlextNet에서 대충 Conv2D를 어떻게 사용하는지 감이 왔다면, ResNet을 한번 구현해 보자.

ResNet에 대한 자세한 설명은 다른 포스트에서 정말 이게 맞나 싶을 정도로 분해해서 설명하도록 하겠다. 지금은 그저 다음과 같은 구조가 있구나 정도만 이해하고 넘어가면 된다.

이것이 ResNet50의 구조인데, 2가지 layer를 구현해 보아야 한다. 첫번째는 Conv Block이고 두번째는 Identity Block이다. 하나는 Skip Connection에 Convolution layer를 입힌 것이고 다른 하나는 그렇지 않은 것 뿐이다.

Residual Conv Block

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35

class ResidualConvBlock(tfk.layers.Layer):
    def __init__(self, InputChannel, OutputChannel, strides = (1, 1), trainable=True, name=None, dtype=None, dynamic=False, **kwargs):
        super().__init__(trainable=trainable, name=name, dtype=dtype, dynamic=dynamic, **kwargs)

        self.Batch1 = tfk.layers.BatchNormalization(momentum=0.99, epsilon= 0.001)
        self.conv1 = tfk.layers.Conv2D(filters=InputChannel, kernel_size=(1, 1), strides=strides)
        self.LeakyReLU1 = tfk.layers.LeakyReLU()
        self.Batch2 = tfk.layers.BatchNormalization(momentum=0.99, epsilon= 0.001)
        self.conv2 = tfk.layers.Conv2D(filters=InputChannel, kernel_size=(3, 3), strides=(1, 1), padding="SAME")
        self.LeakyReLU2 = tfk.layers.LeakyReLU()
        self.Batch3 = tfk.layers.BatchNormalization(momentum=0.99, epsilon= 0.001)
        self.conv3 = tfk.layers.Conv2D(filters=OutputChannel, kernel_size=(1, 1), strides=(1, 1))
        self.LeakyReLU3 = tfk.layers.LeakyReLU()

        # Skip Connection
        self.SkipConnection = tfk.layers.Conv2D(filters=OutputChannel, kernel_size=(1, 1), strides=strides)
        self.SkipBatch = tfk.layers.BatchNormalization(momentum=0.99, epsilon= 0.001)
        self.LeakyReLUSkip = tfk.layers.LeakyReLU()

    def call(self, Input):
        Skip = Input
        Skip = self.SkipConnection(Skip)
        Skip = self.SkipBatch(Skip)
        Skip = self.LeakyReLUSkip(Skip)
        Z = Input
        Z = self.conv1(Z)
        Z = self.Batch1(Z)
        Z = self.LeakyReLU1(Z)
        Z = self.conv2(Z)
        Z = self.Batch2(Z)
        Z = self.LeakyReLU2(Z)  
        Z = self.conv3(Z)
        Z = self.Batch3(Z)
        Z = self.LeakyReLU3(Z)
        return Z + Skip 

Residual Identity Block

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27

class ResidualIdentityBlock(tfk.layers.Layer):
    def __init__(self, InputChannel, OutputChannel, trainable=True, name=None, dtype=None, dynamic=False, **kwargs):
        super().__init__(trainable=trainable, name=name, dtype=dtype, dynamic=dynamic, **kwargs)
        self.Batch1 = tfk.layers.BatchNormalization(momentum=0.99, epsilon= 0.001)
        self.conv1 = tfk.layers.Conv2D(filters=InputChannel, kernel_size=(1, 1), strides=(1, 1))
        self.LeakyReLU1 = tfk.layers.LeakyReLU()
        self.Batch2 = tfk.layers.BatchNormalization(momentum=0.99, epsilon= 0.001)
        self.conv2 = tfk.layers.Conv2D(filters=InputChannel, kernel_size=(3, 3), strides=(1, 1), padding="SAME")
        self.LeakyReLU2 = tfk.layers.LeakyReLU()
        self.Batch3 = tfk.layers.BatchNormalization(momentum=0.99, epsilon= 0.001)
        self.conv3 = tfk.layers.Conv2D(filters=OutputChannel, kernel_size=(1, 1), strides=(1, 1))
        self.LeakyReLU3 = tfk.layers.LeakyReLU()
    
    def call(self, Input):
        Skip = Input
        Z = Input
        Z = self.conv1(Z)
        Z = self.Batch1(Z)
        Z = self.LeakyReLU1(Z)
        Z = self.conv2(Z)
        Z = self.Batch2(Z)
        Z = self.LeakyReLU2(Z)  
        Z = self.conv3(Z)
        Z = self.Batch3(Z)
        Z = self.LeakyReLU3(Z)
        # Z : 256
        return Z + Skip

우선 이 또한 정말이지 Model Subclassing을 그지같이 사용한 예시중 하나이다. 부디 독자들은 이따구로 구현할거면 그냥 Functional API를 사용하기 바란다.

이쯤되면 이런 질문이 나올 것이다.

Q: 왜 저게 그지같이 구현한 예시인가요?
A: 여러 이유가 있지만, 가장 큰 이유는 굳이 모델(Weight)의 정의와 호출을 분리할 이유가 전혀 없는 구조이기 때문입니다.

여기까지 잘 따라왔다면 이제 이 2개의 layer를 사용해서 ResNet50을 다음과 같이 구현할 수 있다.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67

class ResNet50(keras.Model):
    def __init__(self):
        super().__init__()
        # Input Shape 224*224*3
        # Conv 1 Block
        self.ZeroPadding1 = keras.layers.ZeroPadding2D(padding=(3,3))
        self.Conv1 = keras.layers.Conv2D(filters = 64, kernel_size=(7, 7), strides=(2, 2))
        self.Batch1 = keras.layers.BatchNormalization()
        self.ReLU1 = keras.layers.LeakyReLU()
        self.ZeroPadding2 = keras.layers.ZeroPadding2D(padding=(1,1))

        self.MaxPool1 = keras.layers.MaxPool2D(pool_size=(3, 3), strides=2)
        self.ResConvBlock1 = ResidualConvBlock(64, 256, strides = (1, 1))
        self.ResIdentityBlock1 = ResidualIdentityBlock(64, 256)
        self.ResIdentityBlock2 = ResidualIdentityBlock(64, 256)

        self.ResConvBlock2 = ResidualConvBlock(128, 512, strides = (2, 2))
        self.ResIdentityBlock3 = ResidualIdentityBlock(128, 512)
        self.ResIdentityBlock4 = ResidualIdentityBlock(128, 512)
        self.ResIdentityBlock5 = ResidualIdentityBlock(128, 512)

        self.ResConvBlock3 = ResidualConvBlock(256, 1024, strides = (2, 2))
        self.ResIdentityBlock6 = ResidualIdentityBlock(256, 1024)
        self.ResIdentityBlock7 = ResidualIdentityBlock(256, 1024)
        self.ResIdentityBlock8 = ResidualIdentityBlock(256, 1024)
        self.ResIdentityBlock9 = ResidualIdentityBlock(256, 1024)
        self.ResIdentityBlock10 = ResidualIdentityBlock(256, 1024)

        self.ResConvBlock4 = ResidualConvBlock(512, 2048, strides = (1, 1))
        self.ResIdentityBlock11 = ResidualIdentityBlock(512, 2048)
        self.ResIdentityBlock12 = ResidualIdentityBlock(512, 2048)
        
        self.GAP = keras.layers.GlobalAveragePooling2D()
        self.DenseOut = keras.layers.Dense(1000, activation='softmax')

    def call(self, Input):
        X = self.ZeroPadding1(Input)
        X = self.Conv1(X)
        X = self.Batch1(X)
        X = self.ReLU1(X)
        X = self.ZeroPadding2(X)

        X = self.MaxPool1(X)
        X = self.ResConvBlock1(X)
        X = self.ResIdentityBlock1(X)
        X = self.ResIdentityBlock2(X)

        X = self.ResConvBlock2(X)
        X = self.ResIdentityBlock3(X)
        X = self.ResIdentityBlock4(X)
        X = self.ResIdentityBlock5(X)

        X = self.ResConvBlock3(X)
        X = self.ResIdentityBlock6(X)
        X = self.ResIdentityBlock7(X)
        X = self.ResIdentityBlock8(X)
        X = self.ResIdentityBlock9(X)
        X = self.ResIdentityBlock10(X)

        X = self.ResConvBlock4(X)
        X = self.ResIdentityBlock11(X)
        X = self.ResIdentityBlock12(X)

        X = self.GAP(X)
        Out = self.DenseOut(X)
        
        return Out

여기서 하나 GAP로 정의된 Global Average Pooling layer가 있다. 이것에 대해서 간단하게만 알아보자.

이 layer는 단순하게 말하자면 feaeture map을 1차원을 만들어 주는 layer이다. 대개, Image는 3차원인데, 차원별로 존재하는 image를 하나의 Scalar 값으로 만든다는 뜻이다. (Global Pooling) 그때, Scalar 값으로 만드는 과정에서 이미지의 각 픽셀 값을 평균을 내는 방법을 취한 것 뿐이다. (Average)

이를 간단히 그림으로 표현하자면 다음과 같다.

그림에서 보여지는 것과 같이, 각 채널에 있는 이미지들의 픽셀값을 평균을 내서 그것을 모으면 채널의 개수 만큼의 크기를 가지는 1-dimensional vector가 완성된다.

여기까지 Convolutional Neural Network의 구현 실습을 마치도록 하겠다. 부디 도움이 되었….을까?는 모르겠지만 재밌게 보았으면 좋겠다.